3. Matrix und ähnliche Umgebungen | LaTeX-Handbuch
Es gibt eine Reihe von Umgebungen zum Setzen von Matrix-ähnlichen Strukturen, die im Paket amsmath definiert sind. Sie ähneln alle in Syntax und Layout der Standard-LaTeX-Array-Umgebung. Im Allgemeinen können verschiedenste zweidimensionale mathematische Strukturen und tabellarische Layouts als Arrays beschrieben werden.
Drei Umgebungen – „cases“, „matrix“ und „pmatrix“ – ersetzen die Befehle von Standard-LaTeX. Die Standardbefehle verwenden eine andere Notation und können daher nicht zusammen mit den hier besprochenen Umgebungsformularen verwendet werden. Das Paket amsmath erzeugt eine Fehlermeldung, wenn einer der alten Befehle verwendet wird. Wenn Sie umgekehrt versuchen, die Formulare der amsmath-Umgebung zu verwenden, ohne das Paket zu laden, erhalten Sie höchstwahrscheinlich die folgende Fehlermeldung: „Fehlplatziertes Tabulatorzeichen &“ für die Ausrichtung.
3.1. Die „Fälle“-Umgebung
Die „Case“-Umgebung wird zur Verarbeitung von Konstruktionen verwendet, bei denen eine einzelne Gleichung mehrere Varianten aufweist. Solche Konstruktionen kommen in der Mathematik sehr häufig vor. Es entsteht ein Array mit zwei Spalten, beide linksbündig.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{equation}
4P_{r - j} = \begin{cases}
5 0 & \text{if $r - j$ is odd,} \\
6r! \, (-1)^{(r - j)/2} & \text{if $r - j$ is even.}
7\end{cases}
8\end{equation}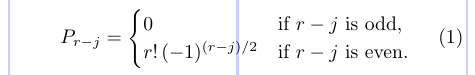
Beachten Sie die Verwendung des Befehls „\text“ und des „eingebetteten Mathematikmodus“ in den Textzeichenfolgen.
3.2. Die Matrixumgebungen
Die Matrixumgebungen akzeptieren im Gegensatz zum array von LaTeX kein Argument, das die Formate der Spalten angibt. Stattdessen bieten sie ein Standardformat: bis zu 10 zentrierte Spalten. Auch der Abstand weicht geringfügig von der Standardeinstellung in array ab. Die folgenden Beispiele veranschaulichen die Umgebungen „matrix“, „pmatrix“, „bmatrix“, „Bmatrix“, „vmatrix“ und „Vmatrix“.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{gather*}
4\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \quad \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \\
5\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \quad \begin{Bmatrix} 1 & 0 \\ 0 & -1 \end{Bmatrix} \\
6\begin{vmatrix} a & b \\ c & d \end{vmatrix} \quad \begin{Vmatrix} i & 0 \\ 0 & -i \end{Vmatrix}
7\end{gather*}
Der Zähler „MaxMatrixCols“ bestimmt die maximale Anzahl von Spalten in einer Matrixumgebung. Sie können es mit dem Standard-Zählerbefehl von LaTeX ändern. Der Wert des Längenparameters „\arraycolsep“ bestimmt den Abstand zwischen den Spalten. Genau wie in Standard-Arrays, aber auf beiden Seiten des Arrays wird kein Leerzeichen hinzugefügt. Mehr Spalten machen LaTeX härter und erfordern mehr Ressourcen. Das Festlegen von „MaxMatrixCols“ auf 20 oder höher ist jedoch ohne spürbare Leistungseinbußen möglich, da solche Grenzwerte bei den heutigen typischen TeX-Implementierungen weniger wichtig sind.
1\usepackage{amsmath}
2\setcounter{MaxMatrixCols}{20}
3% -------------------------------------------------------------------------------
4\[
5\begin{Vmatrix}
6\,a&b&c&d&e&f&g&h&i&j &\cdots\,{} \\
7&a&b&c&d&e&f&g&h&i &\cdots\,{} \\
8& &a&b&c&d&e&f&g&h &\cdots\,{} \\
9& & &a&b&c&d&e&f&g &\cdots\,{} \\
10& & & &\ddots&\ddots&\hdotsfor[2]{5}\,{}
11\end{Vmatrix} \]
In diesem Beispiel wird der Befehl „\hdotsfor“ verwendet, um eine Reihe von Punkten in einer Matrix zu erzeugen, die sich über eine bestimmte Anzahl von Spalten erstreckt. Der optionale Parameter (hier 2) kann verwendet werden, um einen Multiplikator für den Standardabstand (3 mathematische Einheiten) zwischen den Punkten anzugeben. Der dünne Leerraum und die Klammergruppe „,{}“ am Ende jeder Zeile sorgen einfach dafür, dass das Layout besser aussieht; Zusammen ergeben sie zwei dünne Räume, etwa 6mu oder 1/3em.
Um eine kleine Inline-Matrix zur Verwendung in Text zu erstellen, können Sie die Umgebung „smallmatrix“ verwenden.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3To show the effect of the matrix on surrounding lines inside a paragraph, we put it here:
4$ \left( \begin{smallmatrix}
51 & 0 \\ 0 & -1
6\end{smallmatrix} \right) $
7and follow it with enough text to ensure that there is at least one full line below the matrix.
Beachten Sie, dass die Textzeilen nicht auseinandergezogen werden, obwohl die Zeile vor der kleinen Matrix Buchstaben mit Unterlängen enthält.
3.3. Stapeln in tiefgestellten und hochgestellten Zeichen
Manchmal müssen Sie möglicherweise mehrere Zeilen tief- oder hochgestellt setzen. Dazu können Sie den Befehl „\substack“ mit „\“ als Zeilenbegrenzer verwenden.
Die „Subarray“-Umgebung ist eine etwas allgemeinere Struktur, die es Ihnen ermöglicht, Linien links oder rechts auszurichten, anstatt sie zu zentrieren.
1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\begin{gather}
4\sum_{\substack{0 \le i \le m \\ 0 < j < n}} P(i, j) \\
5\sum_{\begin{subarray}{l}
6i \in \Lambda \\
70 \le i \le m \\
80 < j < n
9\end{subarray}} P(i, j)
10\end{gather}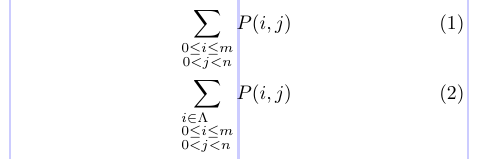
Beachten Sie, dass beide Umgebungen von Klammern umgeben sein müssen, wenn sie als tiefgestellte oder hochgestellte Zahl erscheinen.
3.4. Kommutative Diagramme
Das Paket „amscd“ definiert einige Befehle zum Erstellen einfacher kommutativer Diagramme basierend auf Arrays. Es gibt einige nützliche Kurzformen zur Angabe verzierter Pfeile und anderer Verbindungselemente. Allerdings gibt es Einschränkungen – diese Anschlüsse können beispielsweise nur horizontal oder vertikal sein.
In der „CD“-Umgebung erzeugen die Notationen „@»>“, „@«<“, „@VVV“ und „@AAA“ Pfeile nach rechts, links, nach unten und nach oben. Das folgende Beispiel zeigt auch die Verwendung des Befehls „\DeclareMathOperator“.
1\usepackage{amsmath,amscd}
2\DeclareMathOperator\add{add}
3\DeclareMathOperator\cf {cf}
4\DeclareMathOperator\cov{cov}
5\DeclareMathOperator\non{non}
6% -------------------------------------------------------------------------------
7\[ \begin{CD}
8\cov (L) @>>> \non (K) @>>> \cf (K) \\
9@VVV @AAA @AAA \\
10\add (L) @>>> \add (K) @>>> \cov (K) \\
11\end{CD} \]
Sehen wir uns an, wie Dekorationen spezifiziert werden. Bei den horizontalen Pfeilen wird Material zwischen dem ersten und zweiten „>“- oder „<“-Symbol hochgestellt und Material zwischen dem zweiten und dritten Symbol tiefgestellt. Ebenso wird Material zwischen dem ersten und zweiten oder zweiten und dritten „A“ oder „V“ der vertikalen Pfeile als linkes oder rechtes „Seitenskript“ gesetzt. Wir werden die Verwendung dieses Formats im nächsten Beispiel sehen.
Die Notationen „@=“ und „@|“ ergeben horizontale und vertikale Doppellinien.
Anstelle eines sichtbaren Pfeils können Sie einen „Nullpfeil“ („@.“) verwenden, um ein Array an den erforderlichen Stellen auszufüllen.
1\usepackage{amsmath, amscd}
2\DeclareMathOperator{\End}{End}
3% -------------------------------------------------------------------------------
4\[ \begin{CD}
5S^{W_\Lambda}\otimes T @>j>> T \\
6@VVV @VV{\End P}V \\
7(S \otimes T)/I @= (Z\otimes T)/J
8\end{CD} \]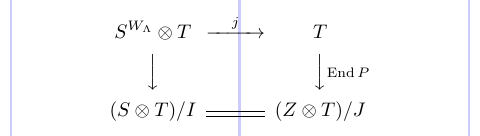
Ein ähnliches Layout kann in Standard-LaTeX erstellt werden. Aber es sieht nicht so gut aus.
1\[\begin{array}{ccc}
2S^{\mathcal{W}_\Lambda}\otimes T & \stackrel{j}{\longrightarrow} & T \\
3\Big\downarrow & & \Big\downarrow\vcenter{\rlap{$\scriptstyle{\mathrm{End}}\,P$}} \\
4(S\otimes T)/I & = & (Z\otimes T)/J
5\end{array}\]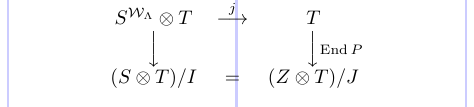
Dieses Beispiel zeigt ganz deutlich, wie viel bessere Ergebnisse das Paket „amscd“ liefert: Die Notation ist einfacher, die horizontalen Pfeile sind länger, der Abstand zwischen Elementen ist deutlich verbessert. Mit den spezielleren Paketen erzielen Sie noch schönere Ergebnisse.
3.5. Trennzeichen, die ein Array umgeben: das Paket „delarray“.
In diesem Abschnitt besprechen wir eine nützliche allgemeine Erweiterung des Pakets array. Mit dieser Erweiterung kann der Benutzer öffnende und schließende erweiterbare Trennzeichen angeben, um eine mathematische array-Umgebung zu umgeben. Schauen wir uns das Beispiel an:
1\usepackage{delarray}
2% -------------------------------------------------------------------------------
3\[ \mathcal{Q} =
4\begin{array}[t] ( {cc} ) X & Y \end{array}
5\begin{array}[t] [ {cc} ] A & B \\ C & D \end{array}
6\begin{array}[b] \lgroup{cc}\rgroup L \\ M \end{array}
7\]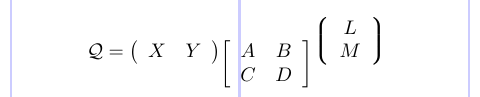
Beachten Sie, dass das Paket „delarray“ unabhängig von
amsmathist, aber bei Bedarf automatisch das Paketarraylädt.
Die Trennzeichen werden auf beiden Seiten von „{cc}“ platziert.
Dieses Beispiel veranschaulicht auch die nützlichste Funktion des Pakets „delarray“: die Verwendung der optionalen Argumente [t] und „[b]“, die in den Matrixumgebungen von amsmath nicht zulässig sind. Diese zeigen, dass die Verwendung der „delarray“-Syntax nicht gleichbedeutend damit ist, die array-Umgebung mit \left und \right zu umgeben, da die Trennzeichen ebenso erhöht werden wie das Array selbst.