Mathematische Formeln verfeinern | LaTeX-Handbuch
Wir haben bereits die meisten Möglichkeiten besprochen, die zum Erstellen mathematischer Formeln erforderlich sind. Aber es gibt noch einige Feinheiten, mit denen Sie wirklich schöne Formeln erstellen können, Formeln, die das Gesamterscheinungsbild und die Lesbarkeit der Bücher und Aufsätze, die Sie tippen, verbessern.
8.1. Interpunktion
Die allgemeine Regel lautet: Wenn auf eine Formel ein Punkt, ein Komma, ein Semikolon, ein Doppelpunkt, ein Fragezeichen, ein Ausrufezeichen usw. folgen, setzen Sie das Satzzeichen nach dem $, wenn die Formel im Text steht; aber setzen Sie das Satzzeichen vor dem „$$“, wenn die Formel angezeigt wird. Zum Beispiel,
1If $x<0$, we have shown that $$y=f(x).$$Sie sollten also niemals so etwas eingeben
1for $x = a, b$, or $c$.Es sollte sein
1for $x = a$, $b$, $c$.Im ersten Fall setzt TeX „$x = a, b$“ als einzelne Formel und setzt so einen dünnen Abstand zwischen dem Komma und dem b. Dieses Leerzeichen ist nicht dasselbe wie das Leerzeichen zwischen Komma und c, da Leerzeichen zwischen Wörtern immer größer sind als dünne Leerzeichen. Ein solcher Abstand sieht schlecht aus, aber im zweiten Fall sieht der Abstand gut aus.
Es ist auch wichtig, dass TeX niemals eine Absatzzeile an der Stelle zwischen dem Komma und dem b umbricht, da Umbrüche nach Kommas in Formeln normalerweise falsch sind, wie in der Gleichung „$x = f(x, a)$“. Dadurch wird die Möglichkeit von Zeilenumbrüchen in einem Absatz verhindert, was zu einem schlechteren Erscheinungsbild des gesetzten Dokuments führt. Mit anderen Worten: Wenn ein Satzzeichen sprachlich eher zum Satz als zur Formel gehört, lassen Sie es außerhalb der $s.
8.2. Nicht kursive Buchstaben
Gängige mathematische Funktionen wie „log“ werden immer in lateinischer Schrift angegeben. Der beste Weg, solche Objekte in eine Formel einzubinden, besteht darin, die folgenden Befehle zu verwenden:

In den folgenden Beispielen werden einige dieser Befehle verwendet:

Die letzten beiden angezeigten Formeln zeigen, dass einige der Befehle von TeX als große Operatoren mit Grenzen wie dem Summenzeichen behandelt werden. Und der Index auf „\max“ wird nicht wie der Index auf „\log“ behandelt. Tiefgestellte und hochgestellte Zeichen werden zu Grenzwerten, wenn sie an „\det“, „\gcd“, „\inf“, „\lim“, „\liminf“, „\limsup“, „\max“, „\min“ angehängt werden , „\Pr“ und „\sup“ im Anzeigestil.
Wenn Sie einen römischen Typ für eine häufig verwendete Funktion oder einen häufig verwendeten Operator benötigen, der oben nicht aufgeführt ist, können Sie ganz einfach Ihren eigenen Befehl definieren. Angenommen, Sie möchten einen Operator mit Grenzen definieren und ihn „\oper“ nennen. Dazu müssen Sie die folgende Definition in die Präambel aufnehmen:
1\def\oper{\mathop{\rm oper}}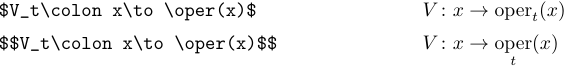
Falls Ihr Operator keine Beschränkungen haben soll, verwenden Sie eine Definition wie die folgende:
1\def\oper{\mathop{\rm oper}\nolimits}Wenn Sie den römischen Typ nur für eine einmalige Verwendung benötigen, ist es einfacher, wie folgt zum Typ „\rm“ zu wechseln:
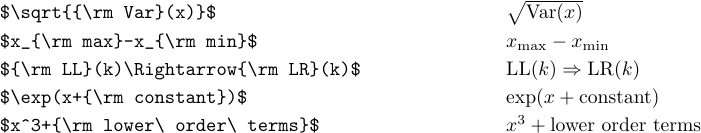
Beachten Sie die Verwendung von „\“ im letzten Fall. Ohne sie wären gewöhnliche Leerzeichen ignoriert worden und „Begriffe niedrigerer Ordnung“ wären als „Begriffe niedrigerer Ordnung“ gesetzt worden.
Das Wort mod, das in Formeln meist auch in lateinischer Schrift gesetzt wird, bedarf einer größeren Sorgfalt, da es auf zwei unterschiedliche Arten verwendet wird. LaTeX bietet den Befehl \bmod, der verwendet wird, wenn mod eine binäre Operation ist, und den Befehl \pmod, der verwendet wird, wenn mod am Ende einer Formel in Klammern steht.
 Beachten Sie, dass
Beachten Sie, dass \pmod seine eigenen Klammern einfügt; Die Menge, die nach mod in diesen Klammern erscheint, sollte in geschweifte Klammern eingeschlossen werden, es sei denn, es handelt sich um ein einzelnes Symbol.
Sie können auch andere Schriftarten auf die gleiche Weise erhalten wie römische Schriftarten, indem Sie „\rm“ verwenden. Beispielsweise ergibt „\bf“ Fettschrift:

Sie können feststellen, dass „+“ und „=“ immer noch in römischer Schrift vorliegen. LaTeX richtet die Dinge so ein, dass Befehle wie „\rm“ und „\bf“ nur die Großbuchstaben „A“ bis „Z“, die Kleinbuchstaben „a“ bis „z“ und die Ziffern „0“ bis „9“ betreffen , die griechischen Großbuchstaben „\Gamma“ bis „\Omega“ und mathematische Akzente wie \hat und „\tilde“. In diesem Beispiel wurden übrigens keine geschweiften Klammern verwendet, da $ eine gruppierende Wirkung haben; „\bf“ ändert die aktuelle Schriftart, aber die Änderung ist lokal, sodass sie sich nicht auf die Schriftart auswirkt, die außerhalb der Formel aktuell war.
Sie können in Formeln auch „\cal“ sagen, um Großbuchstaben im „kalligrafischen“ Stil zu erhalten.

Dies funktioniert nur mit den Buchstaben „A“ bis „Z“. Sie erhalten seltsame Ergebnisse, wenn Sie „\cal“ auf Kleinbuchstaben oder griechische Buchstaben anwenden.
Es gibt auch „\mit“, was für „math italic“ steht. Dies betrifft Großbuchstaben im Griechischen.
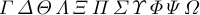
Wenn „\mit“ aktiv ist, werden die gewöhnlichen Buchstaben „A“ bis „Z“ und „a“ bis „z“ nicht geändert; Sie sind wie üblich kursiv geschrieben, da sie normalerweise aus der Schriftart „Math Italic“ stammen. Umgekehrt sind griechische Großbuchstaben und mathematische Akzente von „\rm“ nicht betroffen, da sie normalerweise aus der römischen Schriftart stammen.
Mit LaTeX können Sie auch „\it“ oder „\tt“ eingeben, um den Text kursiv oder in Schreibmaschinenbuchstaben in Ihre Formel einzufügen. Sie fragen sich wahrscheinlich, warum sowohl „\mit“ als auch „\it“ bereitgestellt werden. Die Antwort lautet: „\mit“ ist „math italic“ (was normalerweise am besten für Formeln geeignet ist) und „\it“ ist „text italic“ (was normalerweise am besten für Fließtext geeignet ist).
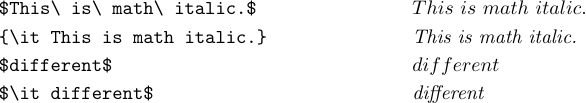
Die mathematischen Kursivbuchstaben sind breiter und der Abstand ist unterschiedlich. Dies funktioniert in den meisten Formeln besser, aber das Erscheinungsbild leidet, wenn Sie versuchen, bestimmte kursive Wörter wie „anders“ im Mathematikmodus einzugeben. Ein breites kursives „f“ ist in Formeln normalerweise wünschenswert, nicht jedoch im Text. Daher ist es am besten, „\it“ in einer Formel zu verwenden, die ein tatsächliches kursives Wort enthalten soll. Dies trifft in der Regel nicht auf die klassische Mathematik zu, kommt aber beim Satz von Computerprogrammen häufig vor:

Das zweite Beispiel zeigt die Verwendung kurzer Unterstreichungen zur Aufteilung von Bezeichnernamen.
8.3. Abstand zwischen Formeln
Es kommt häufig vor, dass eine Anzeige mehr als eine Formel enthält. Beispielsweise kann eine Gleichung von einer Nebenbedingung begleitet sein:
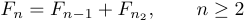
In solchen Fällen müssen Sie TeX mitteilen, wie viel Platz nach dem Komma eingefügt werden soll, da normale Konventionen die Dinge zusammenballen würden. Um dies zu erhalten, können Sie Folgendes eingeben:
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.Hier steht „\qquad“ für „Double Quad“, wobei „Quad“ eine für Drucker übliche Menge an Speicherplatz bedeutet. Somit bedeutet „\quad“ das Quadrat des Raums eines Druckers in horizontaler Richtung. Wenn Sie Abstände wünschen, die von den normalen Konventionen abweichen, müssen Sie diese explizit angeben, indem Sie Befehle wie „\quad“ und „\qquad“ verwenden.
Ein Quad war früher ein quadratisches Stück Rohling, 1 cm breit und 1 cm hoch – ungefähr so groß wie ein großes M; aber das Quad von LaTeX hat keine Höhe.
Im Text eines Absatzes sehen Formeln besser aus, wenn sie durch Wörter und nicht nur durch Kommas getrennt werden. Wenn aber wirklich kein Text einzufügen ist, sollten Sie zumindest etwas Abstand zwischen den Formeln setzen. Vergleichen
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.Und
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.die geben
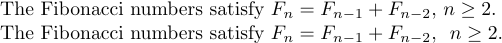
Das „\“ sorgt hier für eine optische Trennung, die den schlechten Stil teilweise ausgleicht.
8.4. Abstände innerhalb von Formeln
Wir haben bereits gesehen, dass TeX automatische Abstände zwischen mathematischen Formeln vornimmt, wodurch diese in den meisten Fällen richtig aussehen. Es ist jedoch natürlich, dass Ausnahmen auftreten, da die Anzahl der möglichen Formeln enorm ist und die Abstandsregeln von TeX recht einfach sind. Daher ist es in solchen Fällen wünschenswert, feine Abstandseinheiten zu haben, anstelle der großen Teile, die aus „\“, „\quad“ und „\qquad“ entstehen.
Die Grundelemente des Raums, die TeX in Formeln einfügt, werden dünne Räume, mittlere Räume und dicke Räume genannt. TeX fügt sie automatisch in Formeln ein, Sie können jedoch jederzeit mit den Befehlen Ihre eigenen Abstände hinzufügen

Formeln mit Analysis sehen am besten aus, wenn vor dx oder dy oder d was auch immer ein extra dünnes Leerzeichen eingefügt wird; aber TeX macht das nicht automatisch. Die folgenden Beispiele zeigen, wie man TeX über diese Bedürfnisse informiert:

Beachten Sie, dass in der vorletzten Formel nach dem „/“ kein „,“ erforderlich war. Im letzten Beispiel ist „\“ auch nicht erforderlich, da dt ganz allein im Zähler eines Bruchs erscheint; Dadurch wird es optisch vom Rest der Formel abgegrenzt.
Physische Einheiten sollten, wenn sie in einer Formel erscheinen, in römischer Schrift angegeben und durch ein dünnes Leerzeichen vom vorhergehenden Material getrennt werden:

Auch nach Ausrufezeichen sollten dünne Leerzeichen eingefügt werden (faktorielle Operation), wenn das nächste Zeichen ein Buchstabe, eine Ziffer oder ein öffnendes Trennzeichen ist:
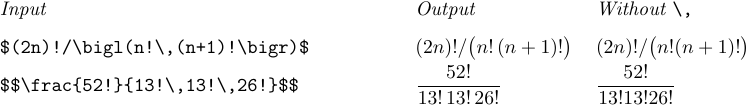
Abgesehen von diesen Fällen werden Sie gelegentlich auf Formeln stoßen, in denen die Symbole aufgrund bestimmter unglücklicher Kombinationen von Formen zu eng aneinandergereiht sind oder bei denen zu viel Leerraum entsteht. Ein geschmackvoll eingesetztes „\“ oder „!“ öffnet oder schließt Dinge, so dass der Leser nicht von der mathematischen Bedeutung der Formel abgelenkt wird. Radikale und multiple Integrale sind häufig Kandidaten für eine solche Feinabstimmung. Hier sind einige Beispiele für Situationen, auf die Sie achten sollten:

Die Abstandsregeln von TeX schlagen manchmal fehl, wenn ‘|’ und ‘\|’ erscheinen in einer Formel, da diese Symbole als gewöhnliche Symbole und nicht als Trennzeichen behandelt werden. Betrachten Sie die Formeln
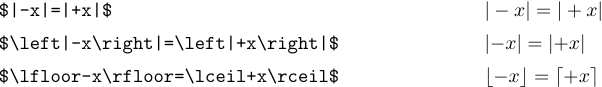
Im ersten Fall ist der Abstand falsch, weil TeX denkt, dass das Pluszeichen die Summe von „|“ berechnet. und ‘x’. Die Verwendung von \left und \right im zweiten Beispiel bringt TeX auf den richtigen Weg. Das dritte Beispiel zeigt, dass bei anderen Trennzeichen keine derartigen Korrekturen erforderlich sind, da TeX weiß, ob es sich um Eröffnungs- oder Schlusszeichen handelt.
8.5. Ellipsen
Eine Ellipse kann durch zwei verschiedene Arten von Punkten angezeigt werden, von denen einer höher als der andere ist. Die besten Überlieferungen unterscheiden zwischen diesen beiden Möglichkeiten. Im Allgemeinen ist es richtig, Formeln wie zu erstellen
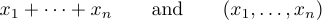
aber falsch, Formeln wie zu produzieren
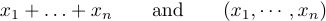
Die Idee besteht darin, \ldots einzugeben, wenn Sie drei niedrige Punkte wünschen, und „\cdots“, wenn Sie drei vertikal zentrierte Punkte wünschen. Im Allgemeinen ist es am besten, „\cdots“ zwischen „+“ und „-“ und Multiplikationszeichen sowie zwischen „=“-Zeichen oder „Kleiner-oder-gleich“-Zeichen oder Teilmengenzeichen oder anderen ähnlichen Beziehungen zu verwenden. Zwischen Kommas werden niedrige Punkte verwendet, und wenn Dinge nebeneinander stehen, ohne dass dazwischen überhaupt ein Zeichen steht:
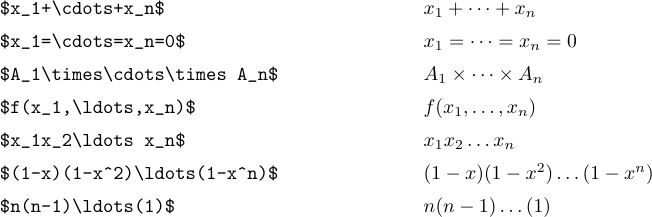 Es gibt jedoch einen Sonderfall, in dem
Es gibt jedoch einen Sonderfall, in dem \ldots und „\cdots“ nicht den richtigen Abstand erzeugen. Dies geschieht, wenn sie ganz am Ende einer Formel oder direkt vor einem schließenden Trennzeichen erscheinen. In solchen Situationen ist ein besonders dünner Raum erforderlich. Betrachten Sie zum Beispiel die folgenden Sätze:
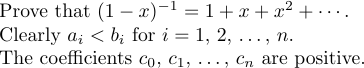
Der erste Satz wird durch Tippen erstellt
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.Ohne das „\“ wäre der Punkt zu nahe an die „\cdots“ herangekommen.
Der zweite Satz wurde wie folgt getippt:
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.Beachten Sie die Verwendung von Bindestrichen („~“), die fehlerhafte Zeilenumbrüche verhindern. Solche Ellipsen sind in einigen Formen des mathematischen Schreibens sehr verbreitet, daher stellt LaTeX das Makro \dots als Abkürzung für „$\ldots,$“ zur Verwendung im Text eines Absatzes bereit. Der dritte Satz kann also getippt werden
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6. Zeilenumbruch
Wenn Sie Formeln in einem Absatz haben, muss TeX diese möglicherweise zwischen den Zeilen umbrechen. Eine Formel wird nur nach einem Beziehungssymbol oder nach einem binären Operationssymbol unterbrochen, wenn sich die Beziehung oder binäre Operation auf der äußeren Ebene der Formel befindet, was bedeutet, dass sie nicht in „{…}“ eingeschlossen ist. Zum Beispiel, wenn Sie tippen
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$In der Mitte des Absatzes besteht die Möglichkeit, dass TeX nach einem der =-Zeichen (bevorzugt) oder nach dem - oder + oder - (im Notfall) abbricht. Es wird aber auf keinen Fall einen Umbruch nach dem Komma geben, da Kommas, nach denen Umbrüche erwünscht sind, nicht zwischen $ stehen sollten.
Wenn Sie in diesem Beispiel keine Unterbrechung zulassen möchten, außer nach den =-Zeichen, können Sie Folgendes eingeben
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$denn diese zusätzlichen Klammern „frieren“ die Unterformeln ein und packen sie in unzerbrechliche Boxen. Aber über solche Dinge müssen Sie sich keine Sorgen machen, es sei denn, TeX verstößt tatsächlich gegen eine Formel, da die Wahrscheinlichkeit dafür ziemlich gering ist.
Wenn Sie das Umbrechen an einem bestimmten Punkt in der äußeren Ebene einer Formel zulassen möchten, können Sie „\allowbreak“ sagen. Wenn zum Beispiel die Formel
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$im Text eines Absatzes erscheint, ermöglicht TeX die Aufteilung in zwei Teile
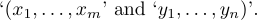
8.7. Zahnspange
Die Symbole { und } werden in verschiedenen Notationen verwendet, und LaTeX bietet einige Befehle, die Ihnen beim Umgang mit Formeln helfen, die solche Dinge beinhalten.
Im einfachsten Fall werden geschweifte Klammern verwendet, um eine Menge von Elementen anzuzeigen. Beispielsweise steht „{a, b, c}“ für die Menge der drei Elemente a, b und c:
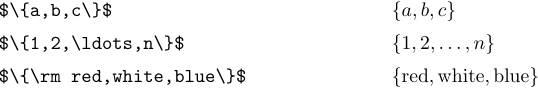
Eine Menge kann auch durch die Angabe eines generischen Elements gefolgt von einer bestimmten Bedingung angegeben werden. Beispielsweise kann die Menge aller Objekte x, die größer als 5 sind, wie folgt geschrieben werden:

Dabei handelt es sich um zwei Varianten, die auf den gleichen Satz hinweisen. Die erste erfordert die Verwendung von „\mid“, um den vertikalen Balken zu erhalten, während die zweite nichts außer dem Doppelpunkt erfordert, der als binäre Operation behandelt wird.
Wenn die Trennzeichen größer werden, sollten sie \bigl, „\bigm“ und „\bigr“ heißen:
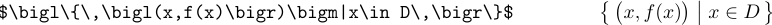
Formeln mit noch größeren Trennzeichen würden die Befehle \big oder \bigg oder sogar \bigg verwenden.
Möglicherweise finden Sie in den angezeigten Formeln auch eine andere Verwendung von geschweiften Klammern. Tatsächlich handelt es sich um eine linke geschweifte Klammer, die eine Auswahl zwischen mehreren Alternativen anzeigt:
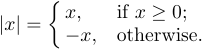
Diese Konstruktion kann mit dem Befehl „\case“ eingegeben werden:
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$Jeder der Fälle besteht aus zwei Teilen, die durch das Symbol „&“ getrennt sind, das beim Aufbau tabellarischer Strukturen eine besondere Rolle spielt. Links vom „&“ befindet sich eine mathematische Formel, die implizit in „$…$“ eingeschlossen ist; Rechts vom „&“ steht normaler Text. Also wird „-x“ in der zweiten Zeile im Mathematikmodus gesetzt, aber „sonst“ wird im horizontalen Modus gesetzt. Leerzeichen vor und nach dem „&“ werden ignoriert. Es kann beliebig viele Fälle geben, in der Regel sind es jedoch nur zwei. Auf jeden Fall sollte „\cr“ folgen.
Horizontale Klammern werden über oder unter Teilen einer angezeigten Formel gesetzt, wenn Sie die Befehle „\overbrace“ oder „\underbrace“ verwenden. Solche Dinge werden als große Operatoren wie \sum betrachtet, daher können Sie durch die Angabe von hoch- oder tiefgestellten Zeichen darüber oder darunter Grenzen setzen:

8.8. Matrizen
Matrizen sind in mathematischen Formeln recht häufige Objekte; Es handelt sich lediglich um rechteckige Arrays von Formeln, die in Zeilen und Spalten angeordnet sind. LaTeX bietet den Befehl „\matrix“, um mit den gängigsten Matrizentypen umzugehen.
Angenommen, Sie möchten die Anzeige festlegen
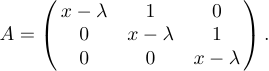
Sie müssen lediglich tippen
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$Dies ist der „\cases“-Konstruktion, die wir zuvor betrachtet haben, ziemlich ähnlich; Jeder Zeile der Matrix folgt ein „\cr“, und zwischen den einzelnen Einträgen jeder Zeile werden „&“-Zeichen verwendet. Anders als bei „\cases“ sollten Sie jedoch Ihre eigenen Trennzeichen \left und \right um die Matrix setzen. Der Grund dafür ist, dass in unterschiedlichen Matrixkonstruktionen unterschiedliche Trennzeichen verwendet werden können. Andererseits werden Klammern häufiger verwendet als andere Trennzeichen, Sie können also „\pmatrix“ eingeben, wenn Sie möchten, dass LaTeX die Klammern für Sie setzt:
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$Jeder Eintrag einer Matrix ist normalerweise in seiner Spalte zentriert, und jede Spalte wird so weit wie nötig erweitert, um die darin enthaltenen Einträge aufzunehmen, und zwischen den Spalten befindet sich ein Abstandsquadrat. Wenn Sie möchten, dass etwas in seiner Spalte links/rechts bündig ausgegeben wird, stellen Sie ihm „\hfill“ voran bzw. stellen Sie es voran.
Jeder Eintrag einer Matrix wird getrennt von den anderen verarbeitet und als mathematische Formel im Textstil gesetzt. Wenn Sie also beispielsweise in einem Eintrag „\rm“ sagen, hat dies keine Auswirkungen auf die anderen. Die Aussage „{\rm x&y}“ ist ungültig.
Matrizen erscheinen oft als generische Muster, die Ellipsen verwenden, um ausgelassene Zeilen oder Spalten anzuzeigen. Sie können solche Matrizen setzen, indem Sie die Ellipsen in eigene Zeilen und/oder Spalten einfügen. Zusätzlich zu \ldots stellt LaTeX für solche Konstruktionen „\vdots“ (vertikale Punkte) und „\ddots“ (diagonale Punkte) zur Verfügung. Betrachten Sie die folgende Matrix
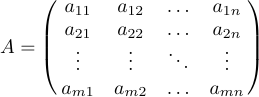
das ist angegeben als:
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$Manchmal ist eine Matrix oben und links von Formeln umrandet, die den Zeilen und Spalten Beschriftungen geben. Für diesen Fall ist in LaTeX ein spezielles Makro namens „\bordermatrix“ definiert. Zum Beispiel das Display
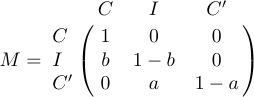
wird beim Tippen erhalten
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$Die erste Zeile enthält die oberen Beschriftungen, die über den großen linken und rechten Klammern erscheinen. Die erste Spalte enthält die linken Beschriftungen, die linksbündig direkt vor der Matrix selbst gesetzt werden. Das Element am Schnittpunkt der ersten Spalte und der ersten Zeile ist normalerweise leer. Und wie „\pmatrix“ fügt „\bordermatrix“ seine eigenen Klammern ein.
Das Einfügen von Matrizen in den Text eines Absatzes ist normalerweise nicht ratsam. Der Grund dafür ist, dass sie so groß sind, dass sie besser angezeigt werden. Dennoch möchten Sie dies vielleicht gelegentlich vernachlässigen. In diesem Fall können Sie „\choose“ oder „\atop“ verwenden:
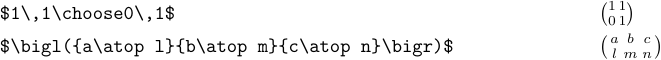
Das Makro „\matrix“ erzeugt keine kleinen Arrays wie dieses.