7. Vorgrößenanpassungen des Layouts | LaTeX-Handbuch

Normalerweise leistet LaTeX hervorragende Arbeit bei der Erstellung mathematischer Formeln. Manchmal ist jedoch eine feinere Anpassung der Positionierung erforderlich. In diesem Artikel werden einige Techniken zur Feinabstimmung des Layouts erläutert, um mathematische Formeln etwas besser zu machen.

7.1. Automatische Größen- und Abstandsanpassung

Mathematische Symbole und Buchstaben werden im Allgemeinen kleiner (und mit engeren Abständen), wenn sie in Brüchen, tiefgestellten oder hochgestellten Zeichen erscheinen. Mathematische Formeln können in acht TeX-Mathe-Stilen angelegt werden:


D, D'	`\displaystyle`	Displayed on lines by themselves
T, T'	`\textstyle`	Embedded in text
S, S'	`\scriptstyle`	In superscripts or subscripts
SS, SS'	`\scriptscriptstyle`	In all higher-order superscripts or subscripts

Der Textstil (T) wird auf der obersten Ebene einer Formel verwendet, die im Fließtext steht (zwischen einem Paar $ oder zwischen $ und $), während der Anzeigestil auf der obersten Ebene einer angezeigten Formel verwendet wird (zwischen einem Paar $$ oder zwischen \[ und \]). Wie bei Unterformeln kann der Stil aus der folgenden Tabelle bestimmt werden:


D	S	S'	T	T'
D'	S'	S'	T'	T'
T	S	S'	S	S'
T'	S'	S'	S'	S'
S, SS	SS	SS'	SS	SS'
S’, SS'	SS'	SS'	SS'	SS'

Das nächste Beispiel veranschaulicht die verschiedenen Stile:

 1\normalsize                 %% Style:
 2\[ b                        %% D
 3    ^0                      %% S
 4   +                        %% D
 5   \frac{(k + p)            %% T
 6          _{j'}             %% S'
 7         % \displaystyle
 8         \pm                %% T [D]
 9         \frac{(f + q)      %% S [T]
10                ^{(pk)      %% SS [S]
11                   ^y       %% SS
12                   _{j'}}}  %% SS'
13              {(h + y)}}    %% S' [T']
14        {(l + q)            %% T'
15          ^{(pk)}}          %% S'
16\]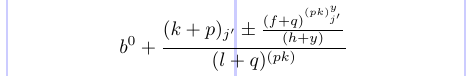

$Verschiedene Mathematikstile$

Sie können das Kommentarzeichen („%“) vor \displaystyle entfernen und sehen, wie sich einige der Stile zu denen in Klammern geändert haben:

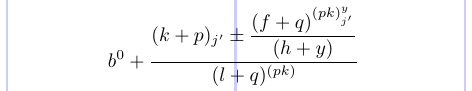
$Explizite geänderte Mathematikstile$

Es zeigt, wie Sie den in jedem Teil zu verwendenden Stil explizit angeben.

7.2. Unterformeln

Im Text gibt ein Klammerpaar eine Gruppe oder einen Bereich an, innerhalb dessen eine Deklaration wirksam ist. Innerhalb einer mathematischen Formel grenzen sie außerdem eine Unterformel ab, die immer als separate Einheit gesetzt und der äußeren Formel hinzugefügt wird. Infolgedessen werden Unterformeln immer in ihrer natürlichen Breite gesetzt und nicht horizontal gedehnt oder verkleinert, wenn TeX einen Absatz aufbaut und versucht, die Formel in eine Zeile einzufügen. Wir haben bereits gezeigt, dass die Unterformel einer einfachen Klammergruppe so verarbeitet wird, als wäre sie ein einzelnes Symbol. Das bedeutet, dass eine leere Gruppe ein unsichtbares Symbol erzeugt, das den Abstand ändern kann.

Der Inhalt von tiefgestellten/hochgestellten Zeichen und die Argumente vieler (aber nicht aller) Befehle, wie z. B. \frac und \mathrel, sind ebenfalls Unterformeln. Somit erhalten sie die gleiche Sonderbehandlung. Das Argument von \bm wird beispielsweise nicht unbedingt als Unterformel festgelegt, und dies ist eine der wichtigen Ausnahmen. Wenn Sie in einer mathematischen Formel nur den Umfang einer Deklaration einschränken müssen, definieren Sie eine Gruppe mit \begingroup und \endgroup. Denken Sie daran, dass spezielle mathematische Deklarationen, wie z. B. Stiländerungen, bis zum Ende der aktuellen Unterformel gelten, unabhängig davon, ob andere Gruppen vorhanden sind oder nicht.

7.3. Große Trennzeichen

LaTeX definiert vier Befehle – \big, \Big, \bigg und „Bigg“, um eine direkte Steuerung der Größe erweiterbarer Trennzeichen zu ermöglichen. Sie nehmen ein einzelnes Argument, das ein erweiterbares Trennzeichen sein muss, und erzeugen größere Versionen des Trennzeichens, vom 1,2- bis 3-fachen der Basisgröße.

Es gibt außerdem drei Varianten für jeden der vier Befehle, die vier Größen des Eröffnungssymbols ergeben (\bigl, \bigl, \biggl und \Biggl). vier Größen von Relationssymbol (\bigm, \Bigm, \biggm und \Biggm); und vier Größen von Schlusssymbolen (\bigr, \Bigr, \biggr und \Biggr). Alle 16 dieser Befehle müssen mit jedem Symbol verwendet werden, das entweder nach \left, \right oder (mit eTeX) \middle stehen kann (siehe diese Tabelle).

Die Größen dieser Trennzeichen sind im Standard-LaTeX festgelegt. Mit dem Paket amsmath passen sich die Größen jedoch an die Größe des umgebenden Materials an, je nach verwendeter Schriftgröße und mathematischem Stil. Dies wird im folgenden Beispiel gezeigt.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
4   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]
5\Large
6\[ \biggl( \mathbf{E}_{y} \int_0^{t_\varepsilon}
7   L_{x, y^x(s)} \varphi(x)\, ds \biggr) \]

$Trennzeichen passen sich der aktuellen Schriftgröße und dem mathematischen Stil an$

7.4. Anpassen des Indexes an einem Radikal

Die Platzierung des Index auf einem Wurzelzeichen ist in Standard-LaTeX nicht immer gut. Sie können jedoch die im Paket amsmath definierten Befehle \leftroot und \uproot verwenden, um die Positionierung dieses Indexes anzupassen. Positive ganzzahlige Argumente für diese Befehle verschieben den Index nach links bzw. oben, während negative Argumente ihn nach rechts und unten verschieben. Diese Argumente werden in mathematischen Einheiten angegeben, die recht klein sind, sodass diese Befehle zur Feinabstimmung geeignet sind.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3\[
4  \sqrt[\beta]{k} \qquad
5  \sqrt[\leftroot{2}\uproot{4} \beta]{k} \qquad
6  \sqrt[\leftroot{1}\uproot{3} \beta]{k}
7\]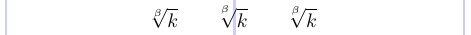

$Anpassen des Index eines Radikalzeichens$

7.5. Feinabstimmung mit Streben und Phantomen

Wann immer Sie den mathematischen Abstand und die Ausrichtung „perfekt“ setzen möchten, ist es in der Regel am besten, auf die einzigartigen und erweiterten Fähigkeiten von primitivem TeX zurückzugreifen. Der Zugriff auf diese Funktionen erfolgt über eine Reihe von Befehlen im Zusammenhang mit \phantom und \smash. Diese Befehle können entweder in mathematischen Formeln oder im Fließtext verwendet werden.

Schauen wir uns das folgende Beispiel an:

 1\usepackage{amsmath}
 2\newcommand\relphantom[1]{\mathrel{\phantom{#1}}}
 3\newcommand\ve{\varepsilon} \newcommand\tve{t_{\varepsilon}}
 4\newcommand\vf{\varphi} \newcommand\yvf{y_{\varphi}}
 5\newcommand\bfE{\mathbf{E}}
 6% -------------------------------------------------------------------------------
 7\begin{equation} \begin{split}
 8  f_{h, \ve}(x, y)
 9    &= \ve \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve u)} \vf(x) \,du  \\
10    &= h \int L_{x, z} \vf(x) \rho_x(dz)                             \\
11    &\relphantom{=} {} + h \biggl[
12       \frac{1}{\tve}
13       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
14               - \tve \int L_{x, z} \vf(x) \rho_x(dz)      \biggr) + \\
15    &\relphantom{=} \phantom{{} + h \biggl[ }
16       \frac{1}{\tve}
17       \biggl( \bfE_{y} \int_0^{\tve}  L_{x, y^x(s)} \vf(x) \,ds
18               - \bfE_{x, y} \int_0^{\tve} L_{x, \yvf(\ve s)}
19                                            \vf(x) \,ds    \biggr) \biggr]
20\end{split} \end{equation}

$Die Phantome der Formel$

Hier wird mit dem Befehl \phantom die horizontale Positionierung angepasst. In der Präambel wird es verwendet, um ein unsichtbares Beziehungssymbol zu definieren, dessen Breite seinem Argument entspricht (in diesem Beispiel „=“). In mathematischen Umgebungen wird es verwendet, um bestimmte Zeilen auszurichten, indem sie mit einer „Phantom“ oder unsichtbaren Unterformel begonnen werden. Das leere Klammerpaar {} ist dasselbe wie \mathord{}, was ein unsichtbares Symbol mit der Breite Null erzeugt, das benötigt wird, um den korrekten Abstand von „+ h“ zu erhalten (ohne {}, das Plus Vorzeichen erzeugt ein unäres Plus mit einem ungeeigneten Abstand vor h).

Im Gegensatz zu \phantom setzt der Befehl \smash seinen Inhalt (in einer LR-Box), ignoriert dann aber sowohl deren Höhe als auch Breite, als ob sie beide Null wären. Der im Standard-LaTeX definierte Befehl \hphantom ist eine Kombination aus beiden. Es erzeugt das Äquivalent von \smash{\phantom{einige Phantominhalte}}, d. h. eine unsichtbare Box mit einer Höhe und Tiefe von Null, aber der Breite des Phantominhalts.

Der Befehl \vphantom ist ähnlich, setzt jedoch die Breite des Phantoms auf Null und behält seine Gesamthöhe plus Tiefe bei. Der Befehl \mathstrut ist als \vphantom( definiert und erzeugt ein Feld mit der Breite Null, dessen Höhe und Tiefe der einer Klammer entsprechen.

Mit dem Paket amsmath kann der Befehl \smash ein optionales Argument annehmen, sodass \smash[t]{...} die Höhe des Inhalts der Box ignoriert und die Tiefe beibehält, während \smash[ b]{...} ignoriert die Tiefe und behält die Höhe bei.

1\usepackage{amsmath}
2% -------------------------------------------------------------------------------
3$\sqrt{x} + \sqrt{y} + \sqrt{z}$ \\
4$\sqrt{x} + \sqrt{\mathstrut y} + \sqrt{z}$ \\
5$\sqrt{x} + \sqrt{\smash{y}} + \sqrt{z}$ \\
6$\sqrt{x} + \sqrt{\smash[b]{y}} + \sqrt{z}$

$Den radikalen Ausdruck zerschlagen$

Es scheint, dass die Radikale ähnlich aussehen, wenn man dem y mit einer Strebe etwas mehr Höhe verleiht. Stattdessen sehen sie dadurch nur noch anders und insgesamt hässlicher aus. Es stellt sich heraus, dass es der beste Weg ist, den Boden des y zu zertrümmern.

Das folgende Beispiel zeigt eine sehr häufige Verwendung von Smashing. Der Befehl \smash wird dort verwendet, um eine genaue Kontrolle über die Höhe der umgebenden Trennzeichen zu ermöglichen. Es zeigt sich auch, dass das Zertrümmern zu Problemen führen kann, da die tatsächliche Höhe der Linie bekannt sein muss. Dies wird von \vphantom repariert. \Hmjd ist das zusammengesetzte Symbol, definiert als:

1\newcommand\Hmjd{\widetilde{\mathcal{H}^2}_{MJD}(\chi)}

Um den resultierenden vertikalen Raum anzuzeigen, haben wir Regeln hinzugefügt:

Aussehen	`Code`	Kommentar
$“Äußere Klammern zu groß”$	`\left( {\Hmjd } \right)`	Äußere Klammern zu groß
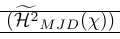$“Äußere Klammern zu klein und Linien zu eng”$	`\left( \smash{\Hmjd } \right)`	Äußere Klammern zu klein und Linien zu eng
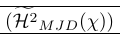$“Genau richtig”$	`\left( \smash[t]{\Hmjd } \right) \vphantom{\Hmjd}`	Genau richtig!
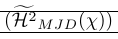$“Sowohl Vphantom als auch Partial Smash erforderlich”$	`\left( \smash[t]{\Hmjd } \right)`	Sowohl `\vphantom` als auch Partial Smash sind erforderlich

An einigen Stellen können Mängel in der TeX-Verarbeitung auf niedriger Ebene zu Fehlern in den Feinheiten des Schriftsatzes führen. Dies kann in bestimmten Layouts passieren, in denen (a) eine Unterformel (Zähler/Nenner eines Bruchs oder tiefgestellter/hochgestellter Index) aus genau einer LR-Box oder einer ähnlich konstruierten mathematischen Box besteht und (b) diese Box nicht ihre natürliche Größe hat, wie bei den komplexeren Formen von \makebox, Schrägstrichen und einigen Phantomen.

Um dies zu sehen, schauen wir uns das folgende Beispiel an:

1\[
2\sqrt{ \frac{a+b}{x_j} } \quad
3\sqrt{ \frac{a+b}{\smash{x_j}} } \quad
4\sqrt{ \frac{a+b}{{}\smash{x_j}} } \quad
5\sqrt{ \frac{a+b}{\smash{x_j+b}} }
6\]

$Probleme durch Smashes$

Um die Tiefe des Radikals zu verringern, wurde im zweiten Radikal ein \smash hinzugefügt, was jedoch keine Wirkung hatte. Im dritten Radikal funktionierte es mit einer leeren Klammergruppe. Aber im vierten Radikal war keine leere Klammergruppe erforderlich. Um es zusammenzufassen: Wenn Sie feststellen, dass \smash nicht funktioniert, versuchen Sie, vor dem einsamen Feld eine leere mathematische Unterformel ({}) einzufügen, damit es richtig behandelt wird.

7.6. Horizontaler Abstand

Für eine feinere und schwierigere Abstimmung sind die in der folgenden Tabelle aufgeführten expliziten Abstandsbefehle erforderlich:

$Horizontale Abstandsbefehle$ Sowohl die Voll- als auch die Kurzform dieser Befehle sind robust und können auch außerhalb mathematischer Formeln in normalem Text verwendet werden. Sie hängen mit den dünnen, mittleren und dicken Leerzeichen zusammen, die auf den Maschinen zur Verfügung standen, die Mitte des 20. Jahrhunderts zum Setzen von Mathematik eingesetzt wurden.

Die aktuellen Werte der drei TeX-Parameter \thinmuskip, \medmuskip und \thickmuskip definieren die Menge an Speicherplatz, die durch diese \..space-Befehle hinzugefügt wird. Ihre Standardwerte mit amsmath sind in der Tabelle aufgeführt. Diese Low-Level-Parameter erfordern Werte in mathematischen Einheiten (mu). Daher können sie nur über TeX-Zuweisungen auf niedriger Ebene festgelegt werden, nicht über \setlength oder ähnliches. Darüber hinaus sollten ihre Werte normalerweise nicht geändert werden, da sie intern vom mathematischen Schriftsatz von TeX verwendet werden (siehe folgende Tabelle).

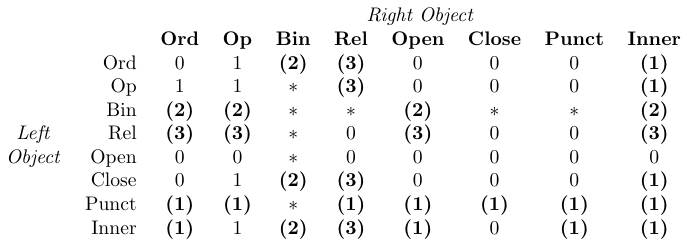
$Abstand zwischen Symbolen$

In der Tabelle bedeutet 0 „kein Leerzeichen“, 1 bedeutet \thinmuspace, 2 bedeutet \medmuskip, 3 bedeutet \thickmuskip, * bedeutet unmöglich. Fettgedruckte Einträge bedeuten, dass in mathematischen Schriftstilen das entsprechende Leerzeichen nicht hinzugefügt wird.

Eine mathematische Einheit (1mu) entspricht 1/18 eines em in der aktuellen mathematischen Schriftgröße. Daraus folgt, dass der absolute Wert eines mu je nach Mathematikstil variiert, sodass unabhängig vom verwendeten Stil ein konsistenter Abstand entsteht.

Text in mathematischen Formeln LaTeX mathe schriftart