9. Symbole in mathematischen Formeln | LaTeX symbole

Die Tabellen in diesem Artikel listen die große Auswahl an mathematischen Symbolen auf, die von den AMS-LATEX-Paketen bereitgestellt werden, einschließlich Befehlen für den Zugriff auf jedes Symbol. Sie enthalten auch die ergänzenden Symbole der von Allan Jeffrey und Jeremy Gibbons entworfenen Schriftart St Mary Road. Dieses Paket erweitert die Symbolschriftsammlungen Computer Modern und AMS und sollte normalerweise zusätzlich zu stmaryrd, aber immer danach, geladen werden. Es bietet zusätzliche Symbole für Bereiche wie funktionale Programmierung, Prozessalgebra, Domänentheorie, lineare Logik und viele mehr.

Die Tabellen geben an, welche zusätzlichen Pakete geladen werden müssen, um die einzelnen Symbolbefehle verwenden zu können. Symbole mit Befehlsnamen in Schwarz sind im Standard-LaTeX verfügbar. Symbole mit Befehlsnamen in Blau erfordern das Laden von amsmath, stmaryrd oder stmaryrd. Bei Bedarf erfolgt eine weitere Klassifizierung durch Markierungen: ^(StM) bedeutet ein Symbol aus stmaryrd, wenn die Tabelle auch Symbole aus anderen Paketen enthält; ^(kernel) markiert Symbole, die in Standard-LaTeX verfügbar sind, jedoch nur durch die Kombination von zwei oder mehr Glyphen, wohingegen ein einzelnes Glyph im angegebenen Paket vorhanden ist; und ^(var) markiert „alphabetische Symbole“ (vom Typ \mathalpha), die ihr Aussehen ändern, wenn sie im Rahmen eines Mathe-Alphabet-Bezeichners verwendet werden.

9.1. Mathematische Symbolklassen

Die primäre Klassifizierung mathematischer Symbole hängt mit ihrer Bedeutung im technischen Gebrauch zusammen. In der mathematischen Typografie definiert diese Klassifizierung das Formellayout. Insbesondere passt der mathematische Formatierer von TeX den horizontalen Abstand auf beiden Seiten jedes Symbols entsprechend seiner mathematischen Klasse an. Diese Klassifizierung macht auch einige feinere Unterscheidungen, zum Beispiel zwischen Akzenten und einfachen Symbolen und indem sie die riesige Liste von Relations-Symbolen in mehrere Tabellen aufteilt.

Der Aufbau für Mathematik ordnet jedes Symbol einer dieser Klassen zu: Ordinary (Ord), Operator (Op), Binary (Bin), Relation (Rel), Opening (Open), Closing (Close) oder Interpunktion (Punct). Die Klasse des Symbols kann explizit geändert werden, indem die Befehle \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathopen und \mathpunct verwendet werden. Im nächsten Beispiel werden \# und \top (beide standardmäßig Ord) in ein Rel und ein Op geändert.

\usepackage[fleqn]{amsmath}
\[ a \# \top _x^\alpha x^\alpha_b \]
\[ a \mathrel{\#} \mathop{\top}_x^\alpha x^\alpha_b \]

Zusätzlich zu den oben genannten Klassen bilden bestimmte Unterformeln – vor allem Brüche und die durch \left und \right erzeugten – eine Klasse namens Inner, die explizit über den Befehl „\mathinner“ verfügbar ist.

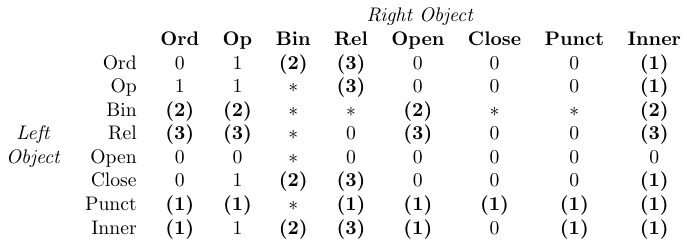
In der Tabelle bedeutet „0“ „kein Leerzeichen“, „1“ bedeutet \thinmuspace, „2“ bedeutet \medmuskip, „3“ bedeutet \thickmuskip, „*“ bedeutet unmöglich. Fettgedruckte Einträge bedeuten, dass in mathematischen Schriftstilen das entsprechende Leerzeichen nicht hinzugefügt wird.

TeX verarbeitet Abstände innerhalb von Formeln, indem es einfach die Klasse jedes Objekts in einer Formel identifiziert und dann Abstand zwischen jedem Paar benachbarter Objekte hinzufügt, wie in der vorherigen Tabelle definiert. Diese Tabelle ist in den mathematischen Satzroutinen von TeX fest codiert und kann daher nicht durch Makropakete geändert werden.

Ein Binär-Symbol wird immer dann in ein Gewöhnliches-Symbol umgewandelt, wenn ihm keine Symbole vorangestellt und gefolgt werden, deren Art mit einer Binäroperation kompatibel ist. Aus diesem Grund sind einige Einträge in der Tabelle als nicht möglich markiert. Beispielsweise ergibt $+x$ +x (ein unäres Plus) und nicht + x. Letzteres kann durch ${}+x$ erzeugt werden.

Betrachten Sie die folgende Formel (die Standardwerte werden geändert, um die hinzugefügten Leerzeichen deutlicher anzuzeigen):

thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[
a - b = -\max \{ x , y \}
\]

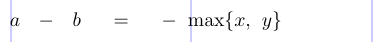
TeX identifiziert die Objekte als Ord, Bin, Ord usw. und fügt dann Leerzeichen wie folgt ein:

 A      -      b      =      -    \max   \{   x    ,       y   \}
Ord \: Bin \: Ord \; Rel \; Ord \, Op   Open Ord Punct \, Ord Close

Das Minus vor „\max“ wird in ein Ordinary umgewandelt, da ein Binary einer Relation nicht folgen kann.

In einer \left...\right-Konstruktion wird die gesamte durch die Konstruktion begrenzte Unterformel zu einem einzelnen Objekt der Klasse Inner. Im Gegensatz dazu erzeugen Befehle wie \bigl und „\Bigr“ jeweils einzelne Symbole der Klassen Opening und Closing. Der Unterschied zwischen ihnen ist in der Abstandstabelle oben ersichtlich. Obwohl sie zu Trennzeichen gleicher vertikaler Größe führen können, kann es je nach benachbarten Objekten in der Formel zu Abstandsunterschieden kommen. Beispielsweise erhält Ordinary, gefolgt von Opening, kein Leerzeichen, wohingegen Ordinary, gefolgt von Inner, durch ein dünnes Leerzeichen getrennt ist. Die Leerzeichen innerhalb der Unterformel innerhalb einer \left...\right-Konstruktion werden wie erwartet erstellt, beginnend mit einem Öffnen-Symbol und enden mit einem Schließen-Symbol.

\thinmuskip=10mu \medmuskip=17mu \thickmuskip=30mu
% -------------------------------------------------------------------------------
\[ a \Bigl( \sum x \Bigr) \neq a \left( \sum x \right) \]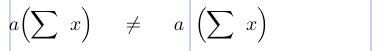

Zusammenfassend lässt sich sagen, dass es besser ist, zu prüfen, ob ein Symbol zur gewünschten Klasse gehört, als es einfach in den folgenden Tabellen nachzuschlagen.

9.2. Buchstaben, Ziffern und andere gewöhnliche Symbole

Die lateinischen ASCII-Buchstaben ohne Akzent und die arabischen Ziffern werden alle als „alphabetische Symbole“ bezeichnet. Die Schriftart, in der sie eingegeben werden, kann variieren. In mathematischen Formeln ist die Standardschriftart für lateinische Buchstaben kursiv, für arabische Ziffern hingegen Hochschrift/Roman. Alphabetische Symbole gehören alle zur Klasse Gewöhnlich.

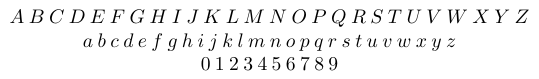
Im Gegensatz zu den lateinischen Buchstaben sind die mathematischen griechischen Buchstaben nicht mehr eng mit den Glyphen verwandt, die zum Setzen normaler griechischer Texte verwendet werden. Aufgrund eines merkwürdigen Zufalls im 18. Jahrhundert ist in der großen europäischen Tradition der mathematischen Typografie die Standardschriftart für griechische Kleinbuchstaben in mathematischen Formeln kursiv, während sie für griechische Großbuchstaben aufrecht/romanisch ist. (In der Physik und Chemie beispielsweise unterscheiden sich die typografischen Traditionen geringfügig.)

Die griechischen Großbuchstaben in den ersten Zeilen der folgenden Tabelle sind ebenfalls alphabetische Symbole, deren Schriftart variiert, wobei die Standardeinstellung Hochformat/Roman ist. Es gibt griechische Großbuchstaben, von denen jeder das gleiche Aussehen wie einige lateinische Buchstaben hat (z. B. A und Alpha, B und Beta, K und Kappa, O und *Omicron). Diese Buchstaben sind in der Tabelle nicht vorhanden. Aus dem gleichen Grund gibt es kein Omikron in Kleinbuchstaben. In der Praxis werden die griechischen Buchstaben, die wie lateinische Buchstaben aussehen, in mathematischen Formeln nicht verwendet.

Symbole in Blau erfordern das Paket stmaryrd. ^(var) zeigt ein variables alphabetisches Symbol an.

In der nächsten Tabelle sind weitere buchstabenförmige Symbole der Klasse Ordinary aufgeführt. Die ersten vier sind hebräische Buchstaben.

Symbole in Blau erfordern das Paket stmaryrd.

Die nächste Tabelle listet die verbleibenden Symbole in der Klasse Ordinary auf, einschließlich einiger gebräuchlicher Satzzeichen. Diese verhalten sich wie Buchstaben und Ziffern, sodass sie um sich herum nie zusätzlichen Platz erhalten.

Symbole in Blau erfordern entweder das Paket amssymb oder, wenn sie mit ^(StM) gekennzeichnet sind, das Paket stmaryrd.

Beachten Sie, dass Ausrufezeichen, Punkt und Fragezeichen in Formeln nicht als Satzzeichen behandelt werden.

Synonyme: logische Negation - \lnot, \neg; | - \vert, |; || - \Vert, \|.

Ein häufiger Fehler besteht darin, diese Symbole direkt als Binär-Operatoren oder Relationssymbole zu verwenden, ohne einen ordnungsgemäß definierten mathematischen Symbolbefehl für diesen Typ zu verwenden. Wenn Sie also Befehle wie \#, \square oder \& verwenden, prüfen Sie sorgfältig, ob Sie die richtigen Leerzeichen zwischen den Symbolen erhalten, oder, noch besser, definieren Sie Ihren eigenen Symbolbefehl.

\usepackage[fleqn]{amsmath} \usepackage{amssymb}
\DeclareMathSymbol\bneg {\mathbin}{symbols}{"3A}
\DeclareMathSymbol\rsquare{\mathrel}{AMSa}{"03}
% -------------------------------------------------------------------------------
\[ a \neg b \qquad x \square y + z \]
\[ a \mathbin{\neg} b \qquad x \mathrel{\square} y + z \]
\[ a \bneg b \qquad x \rsquare y + z \]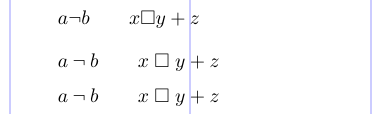

Mit dem Befehl „\DeclareMathSymbol“ können Sie Ihren eigenen Symbolnamen deklarieren.

\DeclareMathSymbol{cmd}{type}{symbol-font}{slot}

Das erste Argument ist der von Ihnen gewählte Befehlsname. Das zweite Argument ist einer der Befehle, die der Symbolklasse entsprechen. Das dritte Argument identifiziert die Symbolschriftart, aus der das Symbol abgerufen werden soll. Das vierte Argument gibt die Position des Symbols in der Schriftartkodierung an, entweder als Dezimal-, Oktal- oder Hexadezimalwert. Die richtigen Werte für die Argumente lassen sich am einfachsten finden, indem man sich die Definitionen in der Datei „amssymb.sty“ oder „fontmath.ltx“ (für die Kernsymbole) ansieht. Wir haben zum Beispiel \neq und \square nachgeschlagen, jeweils das \mathord ersetzt und dem resultierenden Symbol schließlich einen neuen Namen gegeben.

9.3. Mathe-Akzente

In der folgenden Tabelle sind die in Formeln verfügbaren Akzentbefehle aufgeführt. Die meisten davon sind in Standard-TeX definiert. Weitere Informationen zu erweiterbaren Akzenten finden Sie unter hier. Wenn Sie einem Symbol einen mathematischen Akzent hinzufügen, ist das Ergebnis ein Symbol der Klasse Ordinary.

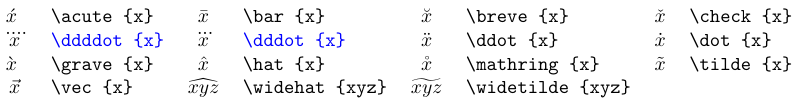
Akzente in Blau erfordern das Paket amsmath.

Die letzten beiden Akzente sind in verschiedenen Breiten verfügbar, wobei automatisch die größte geeignete verwendet wird.

\usepackage{amstext}
% -------------------------------------------------------------------------------
\[ a = b \text{ but } a \tilde{=} b
\text{ which is not } a \mathrel{\tilde{=}} b \]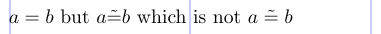

Andere Möglichkeiten, Symbole über Relation-Symbolen zu platzieren, werden hier gezeigt. Wenn Sie in mathematischen Formeln einen Akzent zu einem i oder j hinzufügen, verwenden Sie am besten die punktlosen Varianten \imath und \jmath.

9.4. Binäre Operatorsymbole

Es stehen mehr als 100 Symbole der Klasse Binär zur Auswahl. Die meisten davon sind in der folgenden Tabelle aufgeführt. Einige davon sind auch als Relation-Symbole verfügbar, allerdings unter anderen Namen.

Symbole in Blau erfordern entweder das Paket amssymb oder, wenn sie mit ^(StM) gekennzeichnet sind, das Paket stmaryrd.

Die linken und rechten Dreiecke sind auch als Relations-Symbole verfügbar.

Das Paket stmaryrd ändert verwirrenderweise die Binär-Symbole \bigtriangleup und \bigtriangledown in Operatoren, sodass nur die Synonyme \varbigtriangleup und \varbigtriangledown für die Binär-Operatorformen übrig bleiben.

Das Paket stmaryrd bietet einige Boxsymbole zur Verwendung als Binär-Operatoren; viele weitere werden von stmaryrd hinzugefügt. Siehe nächste Tabelle.

Alle Symbole erfordern entweder das Paket amssymb oder, wenn mit ^(StM) gekennzeichnet, das Paket stmaryrd.

Sie können das Paket stmaryrd mit der Option „heavycircles“ laden. Infolgedessen tauscht jeder Kreissymbolbefehl aus der nächsten Tabelle, der mit \var beginnt, seine Definition mit dem entsprechenden Befehl ohne „var“ aus; Beispielsweise wird das Symbol \varodot zu \odot und umgekehrt.

Symbole in Blau erfordern entweder das Paket amssymb oder, wenn sie mit ^(StM) gekennzeichnet sind, das Paket stmaryrd.

Die Option heavycircles des Pakets stmaryrd betrifft alle Befehle, die mit \var beginnen, und ihre normalen Varianten.

9.5. Beziehungssymbole

Die Klasse der binären Relation-Symbole ist sogar größer als die der Binär-Operatoren. In der nächsten Tabelle sind Symbole für Gleichheit und Ordnung aufgeführt. Ein Schrägstrich kann durch jedes Relation-Symbol gesetzt werden, indem ihm der Befehl „\not“ vorangestellt wird. Das negierte Symbol stellt das Komplement (oder die Negation) der Beziehungen dar.

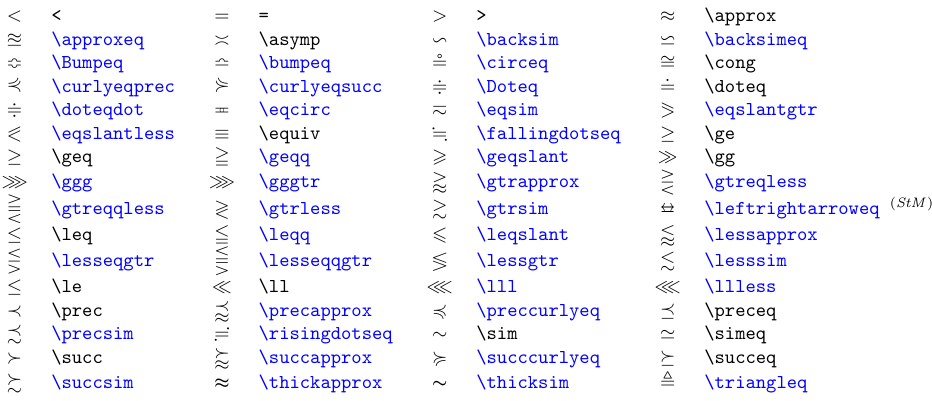
Symbole in Blau erfordern entweder das Paket stmaryrd oder, falls mit ^(StM) gekennzeichnet, das Paket stmaryrd.

$ u \not< v$ or $a \not\in \mathbf{A} $

Diese generische Methode zum Negieren eines Relation-Symbols liefert nicht immer gute Ergebnisse, insbesondere bei größeren Symbolen, da der Schrägstrich immer die gleiche Größe, Position und Steigung hat. Aus diesem Grund stehen auch einige speziell gestaltete „negierte Symbole“ zur Verfügung. Siehe die Liste in der nächsten Tabelle.

Symbole in Blau erfordern das Paket amssymb.

Wenn eine Auswahl verfügbar ist, ist es in der Regel vorzuziehen, die speziell entwickelten Glyphen zu verwenden. Um herauszufinden, warum, vergleichen Sie die Symbole im nächsten Beispiel.

\usepackage{amssymb}
% -------------------------------------------------------------------------------
$ \not\leq \ \not\succeq \ \not\sim $ \par
$ \nleq \ \nsucceq \ \nsim $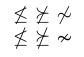

In der nächsten Tabelle sind die Relation-Symbole für Mengen und Einschlüsse aufgeführt.

Symbole in Blau erfordern entweder das Paket amssymboder, wenn mit ^(StM) gekennzeichnet, das Paket stmaryrd.

Und nun Negationen der Relation-Symbole für Mengen und Inklusion.

Symbole in Blau erfordern das Paket amssymb.

In der nächsten Tabelle sind die pfeilförmigen Relation-Symbole aufgeführt. Einige erweiterbare Pfeilkonstruktionen, die zusammengesetzte Relation-Symbole erzeugen, werden hier beschrieben.

Symbole in Blau erfordern entweder das Paket amssymboder, wenn mit ^(StM) gekennzeichnet, das Paket stmaryrd.

Und hier sind die negierten pfeilförmigen Relation-Symbole.

Symbole in Blau erfordern das Paket amssymb.

Es gibt weitere Elemente (zusätzlich zu „\not“, das zum Negieren allgemeiner Relation-Symbole verwendet wird), die speziell zum Negieren oder Erweitern pfeilartiger Symbole entwickelt wurden. Siehe nächste Tabelle.

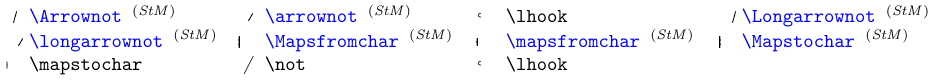
Blaue Symbole erfordern das Paket stmaryrd.

Diese Symbole dienen zum Kombinieren, meist mit Pfeilen; z. B. \longarrownot\longleftarrow.

Verwenden Sie \joinrel, um relationale Symbole zusammenzukleben, z. B. \lhook\joinrel\longrightarrow.

Aufgrund der Abmessungen dieser Symbole sind sie für andere Verwendungen ungeeignet.

\usepackage{stmaryrd}
% -------------------------------------------------------------------------------
$\Longarrownot\longleftrightarrow \qquad \arrownot \hookleftarrow$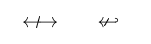

Schließlich finden Sie unten weitere verschiedene Relation-Symbole.

Relations-Symbole in Blau erfordern das Paket amssymb.

\therefore ist ein Relations-Symbol, daher ist sein Abstand bei üblicher Verwendung möglicherweise nicht wie erwartet.