Affiner les formules mathématiques | Manuel LaTeX
Nous avons déjà évoqué la plupart des équipements nécessaires à la construction de formules mathématiques. Mais il reste encore quelques subtilités qui vous permettront de produire de très belles formules, des formules qui amélioreront l’apparence générale et la lisibilité des livres et des articles que vous rédigerez.
8.1. Ponctuation
La règle générale est la suivante : lorsqu’une formule est suivie d’un point, d’une virgule, d’un point-virgule, d’un deux-points, d’un point d’interrogation, d’un point d’exclamation, etc., mettre la ponctuation après le $, lorsque la formule est dans le texte ; mais mettez la ponctuation avant le $$ lorsque la formule est affichée. Par exemple,
1If $x<0$, we have shown that $$y=f(x).$$Donc, vous ne devriez jamais écrire quelque chose comme
1for $x = a, b$, or $c$.Ça devrait être
1for $x = a$, $b$, $c$.Dans le premier cas, TeX composera $x = a, b$ comme une formule unique, mettant ainsi un mince espace entre la virgule et le b. Cet espace ne sera pas le même que l’espace entre la virgule et « c », puisque les espaces entre les mots sont toujours plus grands que les espaces fins. Un tel espacement semble mauvais, mais dans le second cas, l’espacement semblera bon.
Il est également important que TeX ne coupe jamais une ligne d’un paragraphe à l’espace entre la virgule et le « b » car les sauts après les virgules dans les formules sont généralement erronés, comme dans l’équation « $x = f(x, a)$ ». Ainsi, la possibilité de couper des lignes dans un paragraphe est inhibée, ce qui conduit à une pire apparence du document composé. En d’autres termes, si un signe de ponctuation appartient linguistiquement à la phrase plutôt qu’à la formule, laissez-le en dehors des « $ ».
8.2. Lettres non italiques
Les fonctions mathématiques courantes telles que « log » sont toujours définies en caractères romains. La meilleure façon d’inclure de tels objets dans une formule est d’utiliser les commandes suivantes :

Dans les exemples suivants, certaines de ces commandes sont utilisées :

Les deux dernières formules affichées montrent que certaines commandes sont traitées par TeX comme de grands opérateurs avec des limites comme le signe de sommation. Et l’indice sur \max n’est pas traité comme l’indice sur \log. Les indices et exposants deviendront des limites lorsqu’ils seront attachés à \det, \gcd, \inf, \lim, \liminf, \limsup, \max, \min , \Pr et \sup, dans le style d’affichage.
Si vous avez besoin de caractères romains pour une fonction ou un opérateur fréquemment utilisé qui n’est pas répertorié ci-dessus, vous pouvez facilement définir votre propre commande. Supposons que vous souhaitiez définir un opérateur avec des limites et l’appeler « \oper ». Pour ce faire, vous devez inclure la définition suivante dans le préambule :
1\def\oper{\mathop{\rm oper}}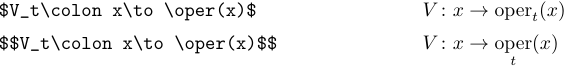
Si votre opérateur n’est pas censé avoir de limites, utilisez une définition comme celle-ci :
1\def\oper{\mathop{\rm oper}\nolimits}Si vous avez besoin du type romain pour un seul usage, il est plus facile de passer au type \rm comme suit :
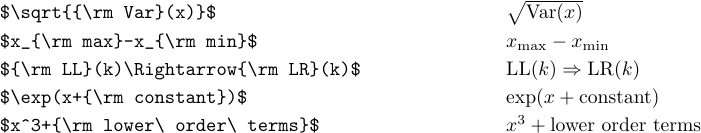
Notez les utilisations de ‘' dans le dernier cas. Sans eux, les espaces vides ordinaires auraient été ignorés et les « termes d’ordre inférieur » auraient été composés comme des « termes d’ordre inférieur ».
Le mot « mod », qui est également généralement écrit en caractères romains dans les formules, nécessite plus de prudence, car il est utilisé de deux manières différentes. LaTeX fournit la commande \bmod à utiliser lorsque “mod” est une opération binaire et la commande \pmod à utiliser lorsque “mod” apparaît entre parenthèses à la fin d’une formule.
 Notez que
Notez que \pmod insère ses propres parenthèses ; la quantité qui apparaît après « mod » entre parenthèses doit être placée entre accolades, sauf s’il s’agit d’un symbole unique.
Vous pouvez également obtenir d’autres styles de caractères de la même manière que vous obtenez des caractères romains en utilisant \rm. Par exemple, \bf donne en gras :

Vous pouvez remarquer que les ‘+’ et ‘=’ sont toujours en caractères romains. LaTeX configure les choses de manière à ce que les commandes comme \rm et \bf n’affectent que les lettres majuscules A à Z, les lettres minuscules a à z, les chiffres 0 à 9 , les lettres grecques majuscules \Gamma à \Omega et les accents mathématiques comme \hat et \tilde. Par ailleurs, aucune accolade n’a été utilisée dans cet exemple, puisque les « $ » ont pour effet de regrouper ; \bf modifie la police actuelle, mais la modification est locale, elle n’affecte donc pas la police qui était actuelle en dehors de la formule.
Vous pouvez également dire « \cal » dans les formules pour obtenir des lettres majuscules dans un style « calligraphique ».

Cela ne fonctionne qu’avec les lettres « A » à « Z » ; vous obtiendrez des résultats étranges si vous appliquez « \cal » à des lettres minuscules ou grecques.
Il y a aussi \mit, qui signifie « math italique ». Cela affecte le grec majuscule.
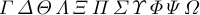
Lorsque \mit est en vigueur, les lettres ordinaires A à Z et a à z ne sont pas modifiées ; ils sont mis en italique comme d’habitude, car ils proviennent généralement de la police italique mathématique. À l’inverse, les lettres grecques majuscules et les accents mathématiques ne sont pas affectés par \rm, puisqu’ils proviennent généralement de la police romaine.
Avec LaTeX, vous pouvez également taper \it ou \tt pour obtenir du texte en italique ou des lettres de machine à écrire dans votre formule. Vous vous demandez probablement pourquoi \mit et \it sont fournis. La réponse est que \mit est “math italic” (ce qui est généralement le meilleur pour les formules), et \it est “text italic” (ce qui est généralement le meilleur pour exécuter du texte).
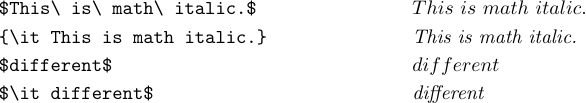
Les lettres mathématiques italiques sont plus larges et l’espacement est différent. Cela fonctionne mieux dans la plupart des formules, mais l’apparence en souffre lorsque vous essayez de taper certains mots en italique comme « différent » en mode mathématique. Un « f » en italique large est généralement souhaitable dans les formules, mais pas dans le texte. Par conséquent, il est préférable d’utiliser « \it » dans une formule censée contenir un véritable mot en italique. Ce n’est généralement pas un cas de mathématiques classiques, mais c’est un cas courant lors de la composition de programmes informatiques :

Le deuxième exemple montre l’utilisation de soulignements courts pour diviser les noms d’identifiant.
8.3. Espacement entre les formules
Il s’agit d’un cas courant lorsqu’un affichage contient plus d’une formule ; par exemple, une équation peut être accompagnée d’une condition secondaire :
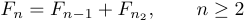
Dans de tels cas, vous devez indiquer à TeX combien d’espace mettre après la virgule, car les conventions normales regrouperaient les choses. Pour l’obtenir, vous pouvez taper
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.Ici, « \qquad » signifie « double quad », où « quad » désigne une certaine quantité d’espace commune aux imprimantes. Ainsi, « \quad » signifie le quad d’espace d’une imprimante dans la direction horizontale. Chaque fois que vous souhaitez un espacement différent des conventions normales, vous devez le spécifier explicitement en utilisant des commandes telles que \quad et \qquad.
Autrefois, un quad était une pièce carrée vierge, mesurant 1 mètre de large et 1 mètre de haut, soit approximativement la taille d’un M majuscule ; mais le quad de LaTeX n’a pas de hauteur.
Dans le texte d’un paragraphe, les formules sont plus belles si elles sont séparées par des mots et non seulement par des virgules. Mais s’il n’y a vraiment pas de texte à insérer, vous devriez au moins mettre un peu d’espace entre les formules. Comparer
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.et
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.qui donnent
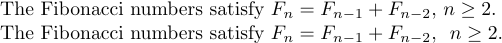
Le ‘' donne ici une séparation visuelle qui compense en partie le mauvais style.
8.4. Espacement dans les formules
Nous avons déjà vu que TeX espace automatiquement les formules mathématiques, ce qui leur donne un aspect correct dans la plupart des cas. Cependant, il est naturel que des exceptions surviennent, car le nombre de formules possibles est énorme et les règles d’espacement de TeX sont assez simples. Il est donc souhaitable d’avoir des unités d’espacement fines pour de tels cas, au lieu des gros morceaux qui proviennent de \ , \quad et \qquad.
Les éléments de base de l’espace que TeX met dans les formules sont appelés espaces fins, espaces moyens et espaces épais. TeX les insère automatiquement dans les formules, mais vous pouvez ajouter votre propre espacement quand vous le souhaitez, en utilisant les commandes

Les formules impliquant du calcul sont plus belles lorsqu’un espace extra fin est inséré avant dx ou dy ou d peu importe ; mais TeX ne le fait pas automatiquement. Les exemples suivants montrent comment informer TeX de ces besoins :

Notez qu’aucun \, n’était nécessaire après le ‘/’ dans l’avant-dernière formule. Il n’est pas non plus nécessaire de \, dans le dernier exemple, puisque le dt apparaît tout seul au numérateur d’une fraction ; cela le détache visuellement du reste de la formule.
Les unités physiques, lorsqu’elles apparaissent dans une formule, doivent être écrites en caractères romains et séparées du matériel précédent par un mince espace :

Des espaces fins doivent également être insérés après les points d’exclamation (opération factorielle), si le caractère suivant est une lettre, un chiffre ou un délimiteur d’ouverture :
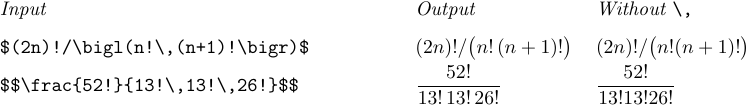
En dehors de ces cas, vous rencontrerez parfois des formules dans lesquelles les symboles sont trop serrés, ou où trop d’espaces blancs apparaissent, à cause de certaines combinaisons de formes malencontreuses. Un «\», ou «!» appliqué avec goût ouvrira ou fermera les choses afin que le lecteur ne soit pas distrait de la signification mathématique de la formule. Les radicaux et les intégrales multiples sont souvent candidats à un tel réglage fin. Voici quelques exemples de situations à surveiller :

Les règles d’espacement de TeX échouent parfois lorsque ‘|’ et ‘\|’ apparaissent dans une formule, car ces symboles sont traités comme des symboles ordinaires plutôt que comme des délimiteurs. Considérez les formules
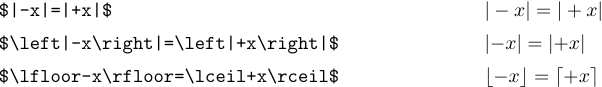
Dans le premier cas, l’espacement est erroné car TeX pense que le signe plus calcule la somme de ‘|’ et ‘x’. L’utilisation de \left et \right dans le deuxième exemple met TeX sur la bonne voie. Le troisième exemple montre qu’aucune correction de ce type n’est nécessaire avec d’autres délimiteurs, car TeX sait s’il s’agit d’ouvertures ou de fermetures.
8.5. Ellipses
Une ellipse peut être indiquée par deux types de points différents, l’un plus haut que l’autre. Les meilleures traditions distinguent ces deux possibilités. Il est généralement correct de produire des formules comme
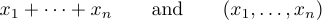
mais c’est mal de produire des formules comme
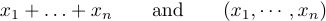
L’idée est de taper \ldots lorsque vous voulez trois points bas, et \cdots lorsque vous voulez trois points centrés verticalement. En général, il est préférable d’utiliser \cdots entre + et - et les signes de multiplication, ainsi qu’entre les signes = ou les signes “inférieur ou égal” ou les signes de sous-ensemble ou d’autres relations similaires. Les points bas sont utilisés entre les virgules, et lorsque les éléments sont juxtaposés sans aucun signe entre eux :
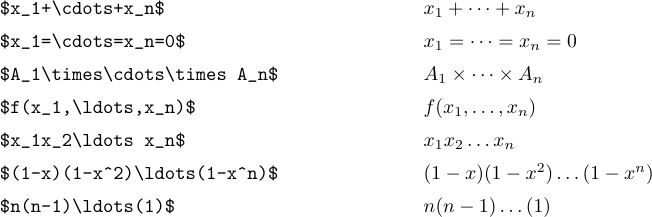 Mais il existe un cas particulier dans lequel
Mais il existe un cas particulier dans lequel \ldots et \cdots ne produisent pas le bon espacement. Cela se produit lorsqu’ils apparaissent à la toute fin d’une formule ou juste avant un délimiteur fermant. Dans de telles situations, un espace très fin est nécessaire. Par exemple, considérons les phrases suivantes :
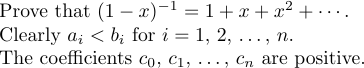
La première phrase est produite en tapant
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.Sans le « \ », le point serait trop proche du « \cdots ».
La deuxième phrase a été tapée comme suit :
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.Notez l’utilisation de liens (~), qui empêchent les mauvais sauts de ligne. De telles ellipses sont très courantes dans certaines formes d’écriture mathématique, c’est pourquoi LaTeX fournit la macro \dots comme abréviation de $\ldots\,$ à utiliser dans le texte d’un paragraphe. La troisième phrase peut donc être tapée
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6. Rupture de ligne
Lorsque vous avez des formules dans un paragraphe, TeX devra peut-être les séparer entre les lignes. Cela brisera une formule uniquement après un symbole de relation, ou après un symbole d’opération binaire, où la relation ou l’opération binaire se trouve au niveau externe de la formule, ce qui signifie qu’elle n’est pas entourée de {...}. Par exemple, si vous tapez
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$au milieu du paragraphe, il y a une chance que TeX se brise après l’un des signes = (de préférence) ou après le - ou + ou - (en cas d’urgence). Mais il n’y aura en aucun cas de saut après la virgule, puisque les virgules après lesquelles les sauts sont souhaitables ne doivent pas apparaître entre les « $ ».
Si vous ne souhaitez pas autoriser la rupture dans cet exemple sauf après les signes =, vous pouvez taper
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$car ces accolades supplémentaires « gèlent » les sous-formules, les plaçant dans des boîtes incassables. Mais il n’y a pas lieu de s’inquiéter de telles choses à moins que TeX ne casse réellement une formule, car la possibilité que cela se produise est assez faible.
Si vous souhaitez autoriser la rupture à un moment donné au niveau externe d’une formule, vous pouvez dire « \allowbreak ». Par exemple, si la formule
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$apparaît dans le texte d’un paragraphe, TeX permettra de le diviser en deux morceaux
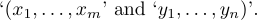
8.7. Croisillons
Les symboles ‘{’ et ‘}’ sont utilisés dans un certain nombre de notations différentes, et LaTeX fournit quelques commandes pour vous aider à gérer les formules impliquant de telles choses. Le cas le plus simple est celui où des accolades sont utilisées pour indiquer un ensemble d’éléments. Par exemple, “{a, b, c}” représente l’ensemble des trois éléments a, b et c :
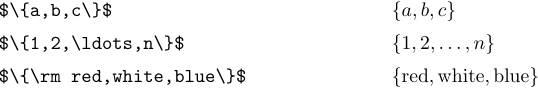
Un ensemble peut également être indiqué en donnant un élément générique suivi d’une condition spécifique. Par exemple, l’ensemble de tous les objets x supérieurs à 5 peut s’écrire comme suit :

Ce sont deux variantes pour indiquer le même ensemble. Le premier nécessite d’utiliser « \mid » pour obtenir la barre verticale, tandis que le second ne nécessite rien d’autre que les deux points, qui sont traités comme une opération binaire.
Lorsque les délimiteurs deviennent plus grands, ils doivent être appelés \bigl, \bigm et \bigr :
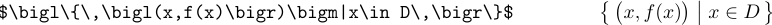
Les formules avec des délimiteurs encore plus grands utiliseraient les commandes \Big ou \bigg ou même \Bigg.
Vous pouvez également trouver une autre utilisation des accolades dans les formules affichées. Il s’agit en fait d’une accolade gauche qui indique un choix entre un certain nombre d’alternatives :
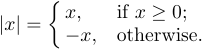
Cette construction peut être tapée à l’aide de la commande \case :
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$Chacun des cas comporte deux parties séparées par le symbole « & », qui joue un rôle particulier dans la construction de structures tabulaires. À gauche du « & » se trouve une formule mathématique qui est implicitement entourée de « $…$ » ; à droite du « & » se trouve un texte ordinaire. Donc -x, dans la deuxième ligne sera composé en mode mathématique, mais le sinon sera composé en mode horizontal. Les espaces vides avant et après le « & » sont ignorés. Il peut y avoir un certain nombre de cas, même s’il n’y en a généralement que deux. Chaque cas doit être suivi de \cr.
Les accolades horizontales seront placées sur ou sous des parties d’une formule affichée si vous utilisez les commandes \overbrace ou \underbrace. De telles choses sont considérées comme de grands opérateurs comme \sum, vous pouvez donc mettre des limites au-dessus ou en dessous d’elles en spécifiant des exposants ou des indices :

8.8. Matrices
Les matrices sont des objets assez courants dans les formules mathématiques ; ce ne sont que des tableaux rectangulaires de formules disposées en lignes et en colonnes. LaTeX fournit la commande \matrix pour gérer les types de matrices les plus courants.
Par exemple, supposons que vous souhaitiez spécifier l’affichage
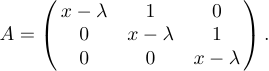
Tout ce que tu fais c’est taper
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$Ceci est assez similaire à la construction \cases que nous avons examinée plus tôt ; chaque ligne de la matrice est suivie de \cr, et les signes & sont utilisés entre les entrées individuelles de chaque ligne. Cependant, contrairement à \cases, vous êtes censé placer vos propres délimiteurs \left et \right autour de la matrice. La raison en est que différents délimiteurs peuvent être utilisés dans différentes constructions matricielles. D’un autre côté, les parenthèses sont utilisées plus souvent que les autres délimiteurs, vous pouvez donc taper \pmatrix si vous souhaitez que LaTeX définisse les parenthèses pour vous :
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$Chaque entrée d’une matrice est normalement centrée dans sa colonne, et chaque colonne s’agrandit autant que nécessaire pour accueillir les entrées qu’elle contient, et il y a un quadruple d’espace entre les colonnes. Si vous voulez que quelque chose ressorte à gauche/droite dans sa colonne, suivez/précédez-le de \hfill.
Chaque entrée d’une matrice est traitée séparément des autres et elle est composée comme une formule mathématique dans le style du texte. Ainsi, par exemple, si vous dites « \rm » dans une entrée, cela n’affecte pas les autres. Dire {\rm x&y} n’est pas valide.
Les matrices apparaissent souvent sous la forme de modèles génériques utilisant des points de suspension pour indiquer les lignes ou les colonnes laissées de côté. Vous pouvez composer de telles matrices en plaçant les ellipses dans leurs propres lignes et/ou colonnes. En plus de \ldots, LaTeX fournit \vdots (points verticaux) et \ddots (points diagonaux) pour de telles constructions. Considérons la matrice suivante
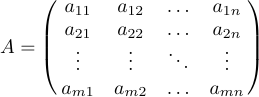
qui est spécifié comme suit :
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$Parfois, une matrice est bordée en haut et à gauche par des formules qui donnent des étiquettes aux lignes et aux colonnes. Pour cette situation, une macro spéciale appelée \bordermatrix est définie dans LaTeX. Par exemple, l’affichage
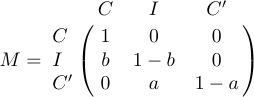
est obtenu lorsque vous tapez
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$La première ligne donne les étiquettes supérieures, qui apparaissent au-dessus des grandes parenthèses gauche et droite ; la première colonne donne les étiquettes de gauche, qui sont composées à gauche, juste avant la matrice elle-même. L’élément à l’intersection de la première colonne et de la première ligne est normalement vide. Et comme \pmatrix, \bordermatrix insère ses propres parenthèses.
Mettre des matrices dans le texte d’un paragraphe est généralement déconseillé. La raison en est qu’ils sont si grands qu’ils sont mieux affichés. Mais il se peut que vous ayez parfois envie de négliger cela. Dans ce cas, vous pouvez utiliser \choose ou \atop :
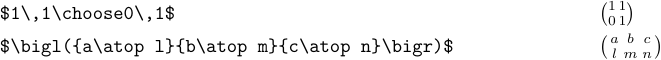
La macro \matrix ne produit pas de petits tableaux comme celui-ci.