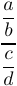Fractions, coefficients binomiaux et styles mathématiques
Une autre chose courante que vous pouvez trouver dans les formules mathématiques sont les fractions et autres constructions où quelque chose comme un numérateur est placé au-dessus de quelque chose comme un dénominateur. Un exemple de ce dernier cas est celui des coefficients binomiaux.
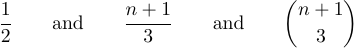
Vous pouvez obtenir ces trois formules sous forme d’équations affichées en tapant $$1\over2$$ et $$n+1\over3$$ et $$\n+1\choose3$$.
La commande \over s’applique à tout ce qui se trouve dans la formule, sauf si vous la placez dans une sous-formule spécifique avec des accolades, auquel cas \over s’applique à tout ce qui se trouve dans cette sous-formule.

Vous ne pouvez pas utiliser \over deux fois dans la même sous-formule, c’est-à-dire taper a\over b\over 2. Au lieu de cela, vous devez spécifier explicitement ce qui dépasse quoi :

Il semble que les deux formules ne soient pas très belles. Dans de tels cas, il est généralement préférable de convertir les fractions sous une « forme barrée ». Par exemple, les deux dernières formules doivent être saisies comme suit :
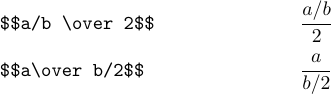
Voici des exemples plus complexes :
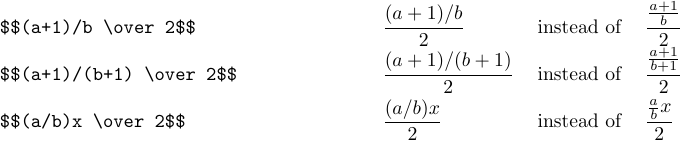
En regardant les exemples ci-dessus, vous avez peut-être remarqué que les lettres et autres symboles deviennent parfois plus petits lorsqu’ils apparaissent sous forme de fractions, tout comme ils deviennent plus petits lorsqu’ils sont en indice ou en exposant. Parlons maintenant de la manière dont TeX choisit la taille des symboles. TeX dispose de huit styles dans lesquels il peut traiter des formules :
- style d’affichage (pour les formules affichées seules sur les lignes)
- style de texte (pour les formules intégrées dans le texte)
- style de script (pour les sous-formules utilisées comme exposants ou indices)
- style scriptscript (pour les exposants ou les indices de second ordre) et quatre styles « étroits » qui sont presque les mêmes, sauf que les indices et les exposants ne sont pas tellement surélevés. Nous appellerons les huit styles D, D’, T, T’, S, S’, SS, SS’, où D est affiché. style, D’ est un style d’affichage exigu, T est un style de texte, etc. TeX utilise également trois tailles pour saisir des formules mathématiques : taille du texte, taille du script et taille du scriptscript.
Pour composer une formule dans un texte en cours d’exécution, vous la placez entre $...$ ; cela produit la formule dans le style T. Ou vous pouvez le mettre entre $$...$$ pour obtenir une formule affichée ; cela affiche la formule dans le style D. Les sous-formules d’une formule peuvent être de styles différents. Une fois que vous connaissez le style, vous pouvez déterminer la taille du type que TeX utilisera :

Il n’y a pas de style “SSS” puisque ces petits symboles seraient encore moins lisibles que ceux du scriptscript.

Par exemple, si x^{a_b} doit être composé dans le style D, le a_b sera défini dans le style S et b dans le style SS ; le résultat est
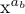
Nous n’avons pas encore vu de différence entre les styles D et T. Il existe en fait une légère différence dans le positionnement des exposants, bien que la taille du script soit utilisée dans chaque cas. Mais il y a une grande distinction entre les styles D et T dans le cas des fractions :

Ainsi, si vous tapez « $1\over2$ » (dans un texte), vous obtenez le style S sur le style S’. Mais si vous tapez $$1\over2$$, vous obtenez le style T sur le style T’ dans une formule affichée.
Enfin, \underline ne change pas le style. Les accents mathématiques et les commandes \sqrt et \overline changent les styles non exigus en leurs homologues exigus conservant les styles exigus.
Il peut arriver que vous n’aimiez pas le style que TeX sélectionne selon ses propres règles. Vous êtes libre de spécifier le style souhaité en tapant \displaystyle ou \textstyle ou \scriptstyle ou \scriptscriptstyle ; le style sélectionné s’appliquera jusqu’à la fin de la formule ou de la sous-formule, ou jusqu’à ce que vous sélectionniez un autre style. Par exemple, $$n+\scriptstyle n+\scriptscriptstyle n.$$ donne l’affichage suivant :
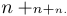
Cela montre que le signe plus devient également plus petit à mesure que le style change et que TeX ne met aucun espace autour du + dans les styles de script.
Jetons un coup d’œil à un autre exemple : une fraction continue.
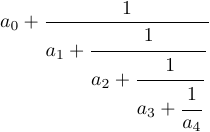
Vous pouvez l’obtenir en tapant
1$$a_0+{1\over\displaystyle a_1+
2 {\strut 1\over\displaystyle a_2+
3 {\strut 1\over\displaystyle a_3+
4 {\strut 1\over a_4}}}}$$Sans \strut et \displaystyle dans cette formule, le résultat serait différent :
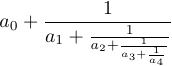
LaTeX définit la macro \frac qui vous permet de spécifier des fractions en utilisant une autre syntaxe : \frac{a}{b} est équivalent à a\over b, et \frac12 est équivalent à 1\over2 .
Il existe une autre opération \atop dans TeX, qui est comme \over sauf qu’elle ne trace pas la ligne de fraction :

Le format LaTeX définit également \choose, qui est comme \atop mais met le résultat entre parenthèses :
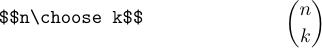
On l’appelle « \choisir » car c’est une notation courante pour le coefficient binomial qui indique combien de façons il existe de choisir k choses parmi n choses.
Les commandes \over, \atop et \choose ne peuvent pas être mélangées entre elles. Par exemple, $$n\choose k\over 2$$ est illégal. Vous devez utiliser le regroupement pour obtenir soit $${n\choose k}\over2$$ ou $$n\choose{k\over2}$$.
TeX a la commande \above qui est une version généralisée de \over et \atop. Dans cette commande, vous spécifiez l’épaisseur exacte de la règle de ligne en tapant \above<dimen>. Par exemple,
1$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$produira une fraction composée avec une règle épaisse de 1 pt entre les fractions du numérateur et du dénominateur :