10. Symboles mathématiques LaTeX et leurs compagnons

Symboles mathématiques LaTeX les plus populaires

Le symbole de sommation LaTeX

L’un des symboles clés fréquemment utilisés dans les équations mathématiques est le symbole de sommation. Dans la section suivante, nous explorerons l’utilisation et le formatage du symbole de sommation dans LaTeX.

Le symbole de sommation, désigné par la lettre grecque Sigma, est utilisé pour représenter l’addition d’une série de termes. Il permet aux mathématiciens d’exprimer de manière concise des concepts tels que les sommes, les séquences et les séries. Dans LaTeX, le symbole de sommation peut être facilement incorporé dans des expressions mathématiques à l’aide de commandes spécifiques.

Utilisation du symbole de somme LaTeX

Pour utiliser le symbole de sommation dans LaTeX, la commande \sum est utilisée. La syntaxe générale est la suivante :

1\sum_{i=lower}^{upper} expression

Ici, la variable i représente l’indice de sommation. Les limites inférieure et supérieure définissent la plage sur laquelle la sommation est effectuée. L’expression, qui peut contenir des termes mathématiques, est ce qui est résumé.

Par exemple, pour représenter la somme des nombres de 1 à 5, le code LaTeX serait :

1$\sum_{i=1}^{5} i$

ce qui donnera le résultat suivant :

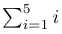
$Un exemple simple de symbole de sommation$

Le symbole de limite LaTeX

Un autre symbole mathématique LaTeX fréquemment utilisé est le symbole de limite LaTeX. Ci-dessous, nous approfondirons sa signification et son utilisation dans les équations mathématiques.

Le symbole de limite LaTeX, souvent noté lim, est un symbole mathématique fondamental utilisé pour décrire le comportement d’une fonction lorsqu’elle s’approche d’une valeur spécifique ou de l’infini. En comprenant les commandes LaTeX associées à ce symbole, les utilisateurs peuvent représenter avec précision les limites de leurs expressions mathématiques.

Utilisation du symbole de limite LaTeX

Pour générer le symbole de limite dans LaTeX, utilisez simplement la commande \lim suivie de toute spécification supplémentaire requise. Par exemple, en tapant

1$\lim_{x \to \infty}f(x)$

produira le symbole de limite avec la variable « x » approchant l’infini comme suit :

$Un exemple de limite simple$

Cette notation indique effectivement que le comportement de la fonction est observé lorsque la variable d’entrée s’approche d’une valeur infiniment grande.

Dans les équations mathématiques, le symbole de limite LaTeX joue un rôle crucial dans l’expression du comportement et des limites des fonctions. Il permet aux chercheurs, aux enseignants et aux étudiants de décrire et d’analyser avec précision des concepts mathématiques tels que la convergence, la continuité et la différentiabilité.

De plus, le symbole de limite LaTeX peut être combiné avec d’autres symboles et opérateurs pour créer des expressions mathématiques plus complexes. Par exemple, l’utilisation du symbole de limite en conjonction avec le symbole de sommation permet aux utilisateurs d’exprimer des sommations avec des limites variables. Cette flexibilité et cette polyvalence font de LaTeX un outil inestimable pour la composition mathématique.

Limites de LaTeX dans la composition mathématique

Les limites des symboles dans LaTeX permettent aux utilisateurs de définir les limites ou les contraintes des expressions mathématiques. Ils sont essentiels pour représenter avec précision des concepts tels que la sommation, l’intégration et les opérations de produit. En utilisant les commandes LaTeX appropriées, les utilisateurs peuvent positionner des limites sur les symboles pour spécifier la plage ou le comportement des opérations mathématiques.

Pour illustrer les limites des symboles dans LaTeX, considérons le symbole de sommation comme exemple. Le symbole de sommation est couramment utilisé pour exprimer la somme d’une série de termes. En utilisant la commande \sum, les utilisateurs peuvent générer le symbole de sommation. Cependant, pour définir les limites de la sommation, des commandes supplémentaires sont nécessaires. Par exemple, en tapant

1$\sum_{i=1}^n$

positionnera l’index inférieur comme « i=1 » et l’index supérieur comme « n ». Cette notation indique que l’opération de sommation doit être effectuée pour les valeurs de i commençant à 1 et se terminant à n.

En plus du positionnement par défaut, LaTeX permet également aux utilisateurs de personnaliser le placement des limites. En utilisant la commande \limits, les utilisateurs peuvent positionner les limites au-dessus et en dessous du symbole de sommation. Par exemple, en tapant

1$\sum\limits_{i=1}^n$

positionnera les limites au-dessus et au-dessous du symbole de somme, fournissant une représentation plus claire. C’est également le comportement par défaut en mode d’affichage. Ainsi

1$$\sum{i=1}^n$$

ne nécessite pas \limits. Mais pour revenir aux limites des positions d’index, \nolimits est requis.

Comparez les variantes dans le tableau ci-dessous :

$Limites des symboles dans différentes positions et modes$

Symbole de grande somme LaTeX

Dans cette section, nous explorerons comment obtenir un symbole de sommation plus grand dans LaTeX en utilisant le package relsize. Avec le package relsize, les utilisateurs peuvent facilement ajuster la taille des symboles mathématiques, y compris le symbole de sommation, pour répondre à leurs besoins spécifiques.

Pour commencer, les utilisateurs doivent inclure le package relsize dans leur document LaTeX en ajoutant la ligne suivante au préambule :

1\usepackage{relsize}

Une fois le package inclus, les utilisateurs peuvent utiliser la commande \mathlarger{} pour obtenir une version plus grande du symbole de sommation. En insérant l’expression souhaitée entre les accolades de \mathlarger{}, le symbole de sommation sera affiché dans une taille plus grande.

Prenons l’exemple suivant :

1\begin{equation*}
2\sin x = \mathlarger{\mathlarger{\sum}}_{n=0}^{\infty}(-1)^n\frac{x^{2n + 1}}{(2n + 1)!}
3\end{equation*}

ce qui donne le résultat ci-dessous :

$Grand symbole de sommation$

Comme nous pouvons le voir, le package relsize dans LaTeX fournit un moyen pratique d’obtenir un symbole de sommation plus grand. En incluant le package dans le préambule du document et en utilisant la commande \mathlarger{}, les utilisateurs peuvent ajuster la taille du symbole de sommation en fonction de leurs besoins spécifiques.

Symboles dans les formules mathématiques LaTeX Tableaux