8. Шрифти в математичних формулах | Математика шрифтів LaTeX
Знайомство зі шрифтами LaTeX
На відміну від плаваючого тексту, зазвичай вам не потрібні автоматичні зміни форми шрифту. Різні фігури мають певне значення в математиці. Наприклад, для векторів можна використовувати жирні вертикальні літери. Якби символи у формулі змінювалися через навколишні умови, результат був би неправильним. Ось чому робота зі шрифтами в математичних формулах відрізняється від обробки тексту.
Символи у формулі можна розділити на два класи: символи та символи алфавіту (включаючи цифри). Насправді TeX внутрішньо має справу з вісьмома класами, які визначають відповідні інтервали. Але для нинішньої дискусії поділу на два класи цілком достатньо.
Деякі символи, наприклад =, можна вводити безпосередньо з клавіатури. Однак частина з них має бути введена за допомогою команди, наприклад, \leq дає знак менше або рівно. Інша основна група символів у формулі, символи алфавіту, вводяться безпосередньо з клавіатури.
Стандартний LaTeX містить більше 200 символів. Це дозволяє користувачеві набирати майже будь-яку бажану формулу. Ці символи розташовані різними шрифтами, але до них можна отримати доступ таким чином, що користувачеві не потрібно знати, як вони представлені всередині. За потреби подібним чином можна зробити доступними додаткові символьні шрифти.
Символи та символи алфавіту мають одну відмінність, яка є для нас зараз найважливішою: символи мають однакове графічне представлення в одній формулі, а користувач може змінювати вигляд символів алфавіту. Команди, які змінюють вигляд символів алфавіту у формулі, називаються математичними алфавітними ідентифікаторами, а шрифти, пов’язані з цими командами, називаються математичними алфавітами. Формула не змінюється, якщо її розміщувати, скажімо, у середовищі теореми, де за замовчуванням текст набирається курсивом, оскільки ідентифікатори алфавіту не залежать від навколишніх команд шрифту поза формулою. Ця поведінка дуже важлива, оскільки форми символів несуть значення, які повинні залишатися незмінними, де б формула не з’являлася в документі.
8.1. Ідентифікатори математичної абетки
Вченим недостатньо одного алфавіту і величезної кількості символів. Вони намагаються використовувати будь-який доступний шрифт для позначення спеціальних понять. На додаток до іноземних алфавітів, таких як грецькі літери, які зазвичай доступні як символи – \alpha, \beta тощо, ми можемо знайти літери без засічок для матриць, жирні літери із засічками для векторів, шрифти Fraktur для груп, ідеали, або поля. Інші використовують каліграфічні форми для позначення наборів. Кількість конвенцій нескінченна, і вони відрізняються від однієї дисципліни до іншої. І LaTeX враховує це, роблячи можливим оголошувати нові ідентифікатори математичних алфавітів і пов’язувати їх із будь-якою бажаною групою форм шрифту замість того, щоб покладатися лише на попередньо визначений набір, який не можна розширити. Ці ідентифікатори є спеціальними командами для використання у формулі, яка набирає будь-який символ алфавіту в своєму аргументі певним шрифтом. Ці ідентифікатори можуть використовувати різні гарнітури в різних формулах, як ми побачимо
пізніше, але в межах однієї формули вони завжди вибирають один і той самий гарнітуру незалежно від оточуючих умов.
Попередньо визначені ідентифікатори алфавіту
LaTeX вже має кілька вбудованих ідентифікаторів алфавіту. Вони показані в таблиці нижче. Останні два рядки показують, що літери, які використовуються у формулах, узяті з математичного алфавіту \mathnormal. З іншого боку, літери, створені за допомогою \mathit, мають різні інтервали, що означає, що цей алфавіт можна використовувати для надання повних імен змінних, які є поширеними в деяких дисциплінах.
| Command | Example code | Result |
|---|---|---|
\mathcal | $\mathcal{A}=a$ | 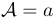 |
\mathrm | $\mathrm{max}_i$ | 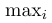 |
\mathbf | $\sum x = \mathbf{v}$ | 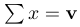 |
\mathsf | $\mathsf{G}_1^2$ | 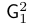 |
\mathtt | $\mathtt{W}(a)$ | 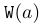 |
\mathnormal | $\mathnormal{abc}=abc$ | 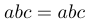 |
\mathit | $differ\neq\mathit{differ}$ | 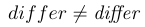 |
У LaTeX2e ідентифікатори математичних алфавітів — це команди з одним аргументом, однією літерою або одним словом, які набираються спеціальним шрифтом.
1Therefore, $\mathsf{G}$ can be computed as
2\begin{equation}
3\mathsf{G} = \mathcal{A} +
4 \sum_{i=1}^{n} \mathcal{B}_{i}
5\end{equation}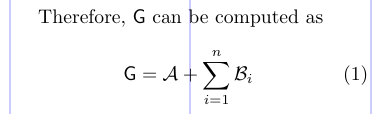
Математичне алфавіт за замовчуванням
Якщо ви не вказуєте ідентифікатор алфавіту явно, з якого алфавіту вибираються символи алфавіту? Іншими словами, який математичний алфавіт є типовим? Відповідь полягає в тому, що єдиного математичного алфавіту за замовчуванням не існує. Систему LaTeX можна налаштувати так, щоб алфавітні символи вибиралися з різних алфавітів, якщо користувач явно не запитує конкретний, і це зазвичай так, як показано в наступному прикладі.
1\begin{eqnarray}
2x &=& 12345 \\
3\mathrm{x} &=& \mathrm{12345} \\
4\mathnormal{x} &=& \mathnormal{12345}
5\end{eqnarray}
Тут ви бачите, що \mathrm не змінює цифри, а \mathnormal не змінює літери, тому за замовчуванням для цифр у звичайному налаштуванні є математичний алфавіт, пов’язаний з \mathrm і за замовчуванням для літер пов’язано з \mathnormal. Цю поведінку можна контролювати за допомогою команди \DeclareMathSymbol.
Який шрифт LaTeX використовує для математики?
У LaTeX типовим шрифтом для математичних режимів є Computer Modern. Однак ви також можете використовувати різні шрифти, вказавши їх у преамбулі документа LaTeX за допомогою пакетів.
Спеціальні ідентифікатори алфавіту
Ви можете використовувати команду \DeclareMathAlphabet, щоб визначити новий ідентифікатор математичного алфавіту. Скажімо, ви хочете зробити похилий шрифт без засічок доступним як математичний алфавіт. Спочатку ви вибираєте нову назву команди, наприклад \msfsl, яка буде використовуватися як ідентифікатор алфавіту. Потім ви зверніться до таблиці класифікації шрифтів, наведеної нижче, щоб знайти відповідну групу форми шрифту для призначення цьому ідентифікатору алфавіту.

Ви побачите, що сімейство Computer Modern Sans, наприклад, складається із середньої серії з вертикальною та похилою формами. Якщо ви вирішите використовувати похилу форму цієї сім’ї, ви повідомите LaTeX за допомогою \DeclareMathAlphabet.
1\DeclareMathAlphabet{cmd}{encoding}{family}{series}{shape}Є чотири параметри (крім самого ідентифікатора) в декларації: назва кодування, сімейство, серія та форма використовуваного шрифту. Ідентифікатор алфавіту, визначений у наступному прикладі, завжди змінюватиметься на Computer Modern Sans із середнім нахилом.
1\DeclareMathAlphabet{\msfsl}{OT1}{cmss}{m}{sl}
2% -------------------------------------------------------------------------------
3We demonstrate this with the formula
4\begin{equation}
5\sum \msfsl{A}_{i} = a \tan \beta
6\end{equation}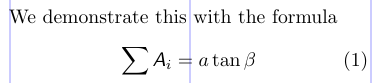
Ви також можете перевизначити існуючий ідентифікатор математичного алфавіту у файлі пакета або в преамбулі вашого документа. Наприклад,
1\DeclareMathAlphabet{\mathsf}{OT1}{pag}{m}{n}замінить налаштування за замовчуванням для ідентифікатора алфавіту \mathsf. Він переключиться на Adobe Avant Garde у ваших формулах.
Note that if the math alphabet in question is part of a symbol font that is already loaded by LaTeX for other reasons (e.g.,
\mathcal), it is better to use\DeclareSymbolFontAlphabetas it makes better use of TeX’s somewhat limited resources for math.
Найкращі математичні шрифти
Окрім стандартного шрифту Computer Modern, LaTeX пропонує сім вбудованих шрифтів для набору математичних алфавітів, тому користувачі можуть налаштовувати свої математичні вирази, не вимагаючи додаткових пакетів у преамбулі. І найкращий варіант для вас – використовувати один із цих 8 шрифтів.
| Font | Usage | Command |
|---|---|---|
| Upright Roman | Standard Upright font | \mathrm{} |
| Calligraphic | Used for typesetting regular mathematics letters. | \mathnormal{} |
| Calligraphic | Used to typeset capital letters with a special Calligraphic font. | \mathcal{} |
| Italic letters | Make the text in italic letters | \mathit{} |
| Upright Sans Serif | Sets upright Sans Serif letters | \mathsf{} |
| Upright Roman boldface | Used for typesetting upright Roman boldface letters | \mathbf{} |
| Typewriter type | Used for for typesetting upright typewriter type letters. | \mathtt{} |
8.2. Команди шрифту тексту в математиці
Хоча оголошення текстових шрифтів, як-от \rmfamily, не можна використовувати в математиці, команди зміни шрифту, наприклад, \textrm, можна використовувати як у тексті, так і в математиці. Використовуючи ці команди, ви можете тимчасово переключитися з математичного контексту на текстовий контекст і набрати текст у середині формули, який логічно є частиною навколишнього тексту поза формулою. Шрифт, який використовується для набору цього тексту, залежатиме від навколишніх умов, що означає, що він успадковуватиме поточне кодування, сімейство, серію та форму, як у прикладі нижче.
1\sffamily The result will be
2\[ x = 10 \textbf{ and thus } y = 12 \]
Тут ми бачимо, що сімейство Sans було збережено, а серію виділено жирним шрифтом. Команда
\text, що надається пакетом amstext (який також завантажується amsmath), може виявитися більш корисною. Він підбирає поточні значення кодування, родини, серії та форми, не змінюючи жодного з них.
8.3. Версії математичних формул
Ми обговорили, як змінити частини формули за допомогою ідентифікаторів математичного алфавіту. LaTeX також дозволяє змінювати зовнішній вигляд формули в цілому. Математичні формули завжди набираються в певній математичній версії. Крім того, ви можете перемикатися між математичними версіями поза математичним режимом за допомогою команди \mathversion, яка змінює загальний макет наступних формул.
LaTeX за замовчуванням має дві математичні версії: звичайну та жирну. А спеціальні пакети надають більше версій. Наприклад, пакет mathtime (для комерційних шрифтів MathTime) встановлює математичну версію під назвою heavy для набору формул із наджирними символами, як це передбачено шрифтами MathTime.
Вочевидь математична версія за замовчуванням — \mathversion{normal}. Жирна версія, у свою чергу, створюватиме жирніші символи алфавіту та символи, хоча великі оператори, такі як \sum, не змінюються за замовчуванням. У прикладі нижче показана та сама формула спочатку у звичайній, а потім у математичній версії, виділеній жирним шрифтом.
1\begin{equation}
2 \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
3\end{equation}
4\mathversion{bold}
5\begin{equation}
6 \sum_{j=1}^{z} j = \frac{z(z+1)}{2}
7\end{equation}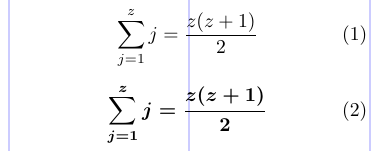
Використання \mathversion може бути доцільним у певних ситуаціях, наприклад у заголовках, але ви повинні пам’ятати, що зміна версії означає зміну вигляду та, можливо, значення всієї формули. Якщо ви хочете затемнити лише деякі символи в одній формулі, вам слід використовувати ідентифікатор алфавіту \mathbf для символів і/або скористатися командою \bm, що надається пакетом
bm, а не змінити \mathversion.
Коли ви змінюєте математичну версію, LaTeX шукає у своїх внутрішніх таблицях, щоб знайти, де розташовані всі символи для цієї нової математичної версії. Він також може змінити всі або деякі ідентифікатори математичного алфавіту та пов’язати їх з іншими формами шрифтів у цій версії.
Але що відбувається з власними ідентифікаторами алфавіту, такими як \msfsl, які ми визначили в
прикладі? Поки ви оголосили їх за допомогою \DeclareMathAlphabet, вони залишатимуться незмінними в усіх математичних версіях.
Якщо ідентифікатор математичного алфавіту має створити інший шрифт у спеціальній математичній версії, ви повинні повідомити про це LaTeX за допомогою команди \SetMathAlphabet. Наприклад, у налаштуваннях за замовчуванням ідентифікатор алфавіту \mathsf визначено таким чином:
1\DeclareMathAlphabet{\mathsf}{OT1}{cmss}{m}{n}
2\SetMathAlphabet{\mathsf}{bold}{OT1}{cmss}{bx}{n}Перший рядок встановлює середовище Computer Modern Sans як значення за замовчуванням для \mathsf у всіх математичних версіях. Другий рядок наказує LaTeX використовувати Computer Modern Sans жирний шрифт, розширений у жирній математичній версії.
1\SetMathAlphabet{cmd}{version}{encoding}{family}{series}{shape}Як ви могли здогадатися з попереднього прикладу, \SetMathAlphabet приймає шість аргументів: ідентифікатор математичного алфавіту, назву математичної версії, для якої ви визначаєте спеціальне налаштування, і чотири параметри для ідентифікації шрифту, з яким ви асоціюєтеся. ваші налаштування.
Як ми зазначали раніше, ви можете перевизначити існуючий ідентифікатор математичного алфавіту за допомогою \DeclareMathAlphabet. Якщо ви це зробите, усі попередні оголошення \SetMathAlphabet для цього ідентифікатора буде видалено з внутрішньої пам’яті LaTeX. Отже, ідентифікатор буде однаковим у всіх математичних версіях, якщо ви не додасте для нього нові оголошення \SetMathAlphabet.
8.4. Налаштування шрифтів у формулах за допомогою пакетів AMS-LATEX
Пакет amsfonts (та amssymb) визначає два математичні алфавіти: алфавіт Euler Fraktur (\mathfrak) і алфавіт Blackboard Bold (\mathbb). Дивіться приклад нижче.
1\usepackage{amsfonts}
2% -------------------------------------------------------------------------------
3$ \forall n \in \mathbb{N} : \mathfrak{M}_n \leq \mathfrak{A} $
5. Напівжирний математичний шрифт. Пакет bm
Тільки для латинських літер ви можете використовувати команду \mathbf. Для всього іншого є пакет bm. Просто завантажте його та використовуйте \bm, щоб зробити будь-яку формулу настільки жирною та красивою, наскільки дозволяють доступні шрифти.
У наступному прикладі показано багато способів використання команд \bm і \mathbf. Він також показує стратегію для визначення скорочених імен для часто зустрічаються жирних символів, використовуючи як стандартні LaTeX \newcommand, так і \bmdefine, які надаються пакетом bm. Зауважте, що \mathbf{xy} не ідентичний \bm{xy}. Перший створює жирний римський “xy”, а другий створює “xy” (жирний математичний курсив).
1\usepackage{amsmath,amssymb,bm}
2\newcommand\bfB{\mathbf{B}} \newcommand\bfx{\mathbf{x}}
3\bmdefine\bpi{\pi} \bmdefine\binfty{\infty}
4% -------------------------------------------------------------------------------
5\section{The bold equivalence
6 $\sum_{j < B} \prod_\lambda : \bm{\sum_{x_j} \prod_\lambda}$}
7\begin{gather}
8 B_\infty + \pi B_1 \sim \bfB_{\binfty} \bm{+} \bpi \bfB_{\bm{1}}
9 \bm {\sim B_\infty + \pi B_1}\\
10 B_\binfty + \bpi B_{\bm{1}} \bm{\in} \bm{\biggl\lbrace}
11 (\bfB, \bfx) : \frac {\partial \bfB}{\partial\bfx}
12 \bm{\lnapprox} \bm{1} \bm{\biggr\rbrace}
13\end{gather}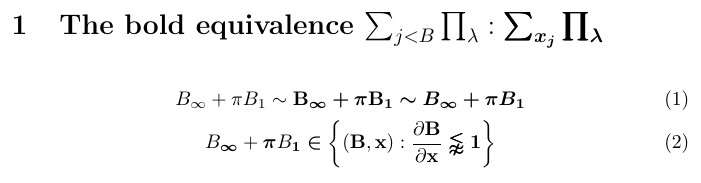
У цьому прикладі bm намагається зробити все можливе, щоб задовольнити запити щодо жирних версій окремих символів і літер. Але якщо придивитися, то побачите, що результати не завжди оптимальні. Наприклад, оператори суми та добутку створюються за допомогою техніки, відомої як жирний шрифт бідняка, у якій символ наноситься тричі з невеликим зсувом. Крім того, фігурні дужки взагалі не виділені жирним шрифтом. Таких недоліків неможливо уникнути, оскільки для деяких символів просто немає жирного варіанту при використанні математичних шрифтів Computer Modern.
Яких точних правил дотримується \bm, щоб створити жирні форми символів у своєму аргументі? Загалом, він використовує той факт, що LaTeX містить жирну математичну версію (доступну через \boldmath) для набору всієї формули жирним шрифтом (за умови наявності та налаштування відповідних жирних шрифтів). Для кожного символу команда \bm переглядає цю математичну версію, щоб побачити, що буде зроблено в цій версії. Якщо шрифт, вибраний для символу, відрізняється від шрифту, вибраного у звичайній математичній версії, символ набирається цим жирним шрифтом, отримуючи ідеальний результат (за умови, що математична версія жирного шрифту налаштована належним чином). Якщо шрифти в обох версіях ідентичні, припускається, що немає доступного варіанту напівжирного шрифту, і використовується напівжирний шрифт бідняка.
Load the
bmpackage after packages that change the existing math font set-up!
Ситуація ще складніша з роздільниками, такими як \biggl\lbrace у прикладі. TeX зазвичай набирає роздільник за допомогою гліфа, вибраного відповідно до запитуваної висоти з послідовності різних розмірів. Ці гліфи можуть бути розташовані різними шрифтами, і певний розмір може мати або не мати жирних варіантів. Все це разом робить неможливим для \bm надійно визначити, чи потрібно йому застосовувати напівжирний шрифт бідняка. Тому він набирає роздільник, використовуючи будь-які шрифти, які пропонує математична версія жирного шрифту. У математичних шрифтах Computer Modern жирним шрифтом доступний лише найменший розмір розділювача; усі інші розміри походять від шрифтів, які не мають жирних варіантів.
1\usepackage{bm}
2% -------------------------------------------------------------------------------
3$\bm{\Biggl\lbrace\biggl\lbrace\Bigl\lbrace\bigl \lbrace \lbrace
4 \mathcal{Q}
5 \rangle \bigr\rangle\Bigr\rangle\biggr\rangle
6\Biggr\rangle}$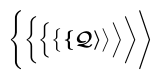 Зазвичай, якщо команда, яка сама приймає аргументи, знаходиться в межах аргументу
Зазвичай, якщо команда, яка сама приймає аргументи, знаходиться в межах аргументу \bm, тоді ця команда має бути повністю включена в аргумент \bm. У результаті всі частини набірного матеріалу будуть виділені жирним шрифтом. Якщо вам потрібно, щоб результат команди з аргументами був лише частково виділений жирним шрифтом, ви повинні зробити наступне. Вам слід розмістити символ(и), які ви не хочете виділяти жирним шрифтом, у \mbox і явно скинути математичну версію у вмісті поля за допомогою \unboldmath. TeX вважає \mbox символом класу Ordinary. Таким чином, щоб отримати правильний інтервал, вам, можливо, доведеться оточити його \mathbin, \mathrel або \mathop.
1\usepackage{amsmath,bm}
2% -------------------------------------------------------------------------------
3$ \bm{\sqrt[2]{x \times \alpha}} $ but
4$ \bm{\sqrt[2]{x \mathbin{\mbox{\unboldmath$\times$}} \alpha}} $
5or the similar
6$ \bm{\sqrtsign}{\bm{x} \times \bm{\alpha}} $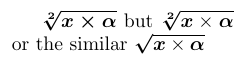
На щастя, такі складні операції потрібні рідко. У більшості випадків команди з аргументами жирним шрифтом потрібно виділяти лише частину аргументу. І цього можна досягти за допомогою команди \bm в цих аргументах. Як і у випадку з \sqrtsign у попередньому прикладі, для звичайного випадку жирних наголосів, \bm спеціально запрограмовано, щоб дозволити аргументу наголосу бути поза його власним аргументом. Однак, якщо вам потрібні такі наголоси регулярно, найкраще визначати власні скорочення, як у прикладі нижче.
Покращення продуктивності
Хоча \bmdefine\bpi{\pi} здається просто скороченням \newcommand\bpi{\bm{\pi}}, насправді правда майже протилежна: \bm визначає новий прихований тимчасовий команду за допомогою \bmdefine, а потім негайно використовує цю тимчасову команду для створення жирного символу. Іншими словами, \bmdefine виконує всю важку роботу! Якщо ви часто використовуєте, наприклад, те, що визначено за допомогою \bm{\alpha}, тоді щоразу виконується новий \bmdefine. Якщо ви надаєте визначення \bmdefine\balpha{\alpha} у преамбулі, то \bmdefine виконує свою трудомістку роботу лише один раз, незалежно від того, скільки разів \balpha використовується.
1\usepackage{bm}
2\bmdefine\bhat{\hat}
3% -------------------------------------------------------------------------------
4$\hat a \neq \bm{\hat a} \neq \bm\hat a = \bhat a\neq \bm\widehat a$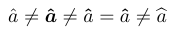
Цей приклад також показує, що акценти змінної ширини (наприклад, \widehat) мають спільний недолік із розділювачами: у математичному налаштуванні Computer Modern вони походять від шрифту, для якого недоступний варіант жирного шрифту.