10. Популярні математичні символи LaTeX та їхні супутники

Найпопулярніші математичні символи LaTeX

Символ підсумовування LaTeX

Одним із ключових символів, які часто використовуються в математичних рівняннях, є символ підсумовування. У наступному розділі ми розглянемо використання та форматування символу підсумовування в LaTeX.

Символ підсумовування, позначений грецькою літерою Sigma, використовується для позначення додавання серії термінів. Це дозволяє математикам стисло виражати такі поняття, як суми, послідовності та ряди. У LaTeX символ підсумовування можна легко включити в математичні вирази за допомогою спеціальних команд.

Використання символу суми LaTeX

Для використання символу підсумовування в LaTeX використовується команда \sum. Загальний синтаксис такий:

1\sum_{i=lower}^{upper} expression

Тут змінна i представляє індекс підсумовування. Нижня та верхня межі визначають діапазон, у якому виконується підсумовування. Вираз, який може містити математичні терміни, є тим, що підсумовується.

Наприклад, щоб представити суму чисел від 1 до 5, код LaTeX буде таким:

1$\sum_{i=1}^{5} i$

що призведе до наступного результату:

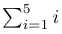
$Приклад простого символу підсумовування$

Символ обмеження LaTeX

Іншим часто використовуваним математичним символом LaTeX є символ обмеження LaTeX. Нижче ми розглянемо його значення та використання в математичних рівняннях.

Символ обмеження LaTeX, який часто позначають як lim, є основним математичним символом, який використовується для опису поведінки функції, коли вона наближається до певного значення або нескінченності. Розуміючи команди LaTeX, пов’язані з цим символом, користувачі можуть точно представляти обмеження у своїх математичних виразах.

Використання символу обмеження LaTeX

Щоб згенерувати символ обмеження в LaTeX, просто скористайтеся командою \lim з наступними додатковими специфікаціями. Наприклад, набір тексту

1$\lim_{x \to \infty}f(x)$

створить граничний символ зі змінною x, що наближається до нескінченності, наступним чином:

$Простий приклад обмеження$

Ця нотація фактично повідомляє, що поведінка функції спостерігається, коли вхідна змінна наближається до нескінченно великого значення.

У математичних рівняннях символ обмеження LaTeX відіграє вирішальну роль у вираженні поведінки та меж функцій. Це дозволяє дослідникам, педагогам і студентам точно описувати й аналізувати такі математичні концепції, як конвергенція, безперервність і диференційованість.

Крім того, символ обмеження LaTeX можна комбінувати з іншими символами та операторами для створення складніших математичних виразів. Наприклад, використання символу обмеження в поєднанні з символом підсумовування дозволяє користувачам виражати підсумовування зі змінними межами. Ця гнучкість і універсальність роблять LaTeX безцінним інструментом для математичного набору.

Обмеження LaTeX у математичному наборі

Обмеження символів у LaTeX дозволяють користувачам визначати межі або обмеження математичних виразів. Вони необхідні для точного представлення таких понять, як підсумовування, інтеграція та операції з продуктом. Використовуючи відповідні команди LaTeX, користувачі можуть установлювати обмеження на символи, щоб визначити діапазон або поведінку математичних операцій.

Щоб проілюструвати обмеження символів у LaTeX, давайте розглянемо символ підсумовування як приклад. Символ підсумовування зазвичай використовується для вираження суми ряду термінів. За допомогою команди \sum користувачі можуть генерувати символ підсумовування. Однак для визначення меж підсумовування потрібні додаткові команди. Наприклад, набір тексту

1$\sum_{i=1}^n$

позиціонуватиме нижній індекс як i=1, а верхній індекс як n. Ця нотація вказує на те, що операцію підсумовування слід виконувати для значень i, починаючи з 1 і закінчуючи n.

На додаток до позиціонування за замовчуванням, LaTeX також дозволяє користувачам налаштовувати розміщення обмежень. Використовуючи команду \limits, користувачі можуть розміщувати обмеження над і під символом підсумовування. Наприклад, набір тексту

1$\sum\limits_{i=1}^n$

розташує межі над і під символом підсумовування, забезпечуючи більш чітке представлення. Це також стандартна поведінка в режимі відображення. Таким чином

1$$\sum{i=1}^n$$

не вимагає \limits. Але щоб повернутися до обмежень у позиціях індексу, потрібен \nolimits.

Порівняйте варіанти в таблиці нижче:

$Обмеження символів у різних положеннях і режимах$

Символ великої суми LaTeX

У цьому розділі ми розглянемо, як отримати більший символ підсумовування в LaTeX за допомогою пакета relsize. За допомогою пакета relsize користувачі можуть легко регулювати розмір математичних символів, включаючи символ підсумовування, відповідно до своїх конкретних потреб.

Для початку користувачі повинні включити пакет relsize у свій документ LaTeX, додавши наступний рядок до преамбули:

1\usepackage{relsize}

Після включення пакета користувачі можуть використовувати команду \mathlarger{}, щоб отримати більшу версію символу підсумовування. Якщо вставити потрібний вираз у фігурні дужки \mathlarger{}, символ підсумовування відображатиметься у більшому розмірі.

Розглянемо такий приклад:

1\begin{equation*}
2\sin x = \mathlarger{\mathlarger{\sum}}_{n=0}^{\infty}(-1)^n\frac{x^{2n + 1}}{(2n + 1)!}
3\end{equation*}

що призводить до результату нижче:

$Великий символ підсумовування$

Як ми бачимо, пакет relsize в LaTeX забезпечує зручний спосіб отримати більший символ підсумовування. Включивши пакет у преамбулу документа та використовуючи команду \mathlarger{}, користувачі можуть налаштувати розмір символу підсумовування відповідно до своїх конкретних потреб.

Математичні символи в LaTeX LaTeX Таблиці